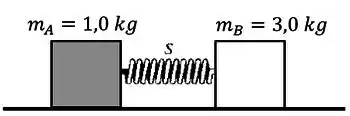
O bloco indicado na figura abaixo possui massa igual a , e o bloco possui massa igual a . Os dois blocos se aproximam, comprimindo a mola entre eles; a seguir o sistema é libertado a partir do repouso sobre uma superfície horizontal sem atrito. A mola possui massa desprezível, não está presa a nenhum dos blocos e cai sobre a mesa depois que ela se expande. O bloco adquire uma velocidade de . Qual a velocidade final do bloco ? Qual foi a energia potencial armazenada na mola comprimida?
Passo 1
Nesse exercício vamos considerar o sistema como os dois blocos e a mola.
Quando eles comprimem a mola, a força elástica vai ser igual nos dois blocos, tendo resultante zero.E como não há ação de forças externas no sistema, isso quer dizer que o momento linear do sistema se conserva
Diferente do normal eu escrevi sem ser na forma vetorial, repara que só vamos ter movimento ao longo da horizontal então o movimento é unidimensional, não preciso usar vetores.
Passo 2
Vamos considerar o momento onde a mola está comprimida ao máximo(momento inicial), e depois o momento que os blocos descolam da mola (momento final).
Vamos considerar o sentido positivo do eixo sendo da esquerda para direita, assim é positivo.
Temos que o momento inicial é zero
Passo 3
Como o momento se conserva temos que o momento final também deve ser zero
Vamos então calcular o momento linear final
Como sabemos que o momento linear final é zero, temos
Passo 4
Como não temos forças dissipativas atuando, como o atrito, a energia mecânica do sistema se conserva
Como no inicio temos só a mola comprimida
E no final temos a mola relaxada e os blocos em movimento
Passo 5
Sendo assim
Resposta