UFRJ, Sem Campus, Física 1, Roteiros de F1 - UFRJ - Roteiro 10 - Colisões, Questão 10a
Uma bola de gude de 10,0 g desloca-se com velocidade de 0,400 m/s para a esquerda sobre uma pista horizontal sem atrito e colide frontalmente com outra bola de gude de 30,0 g que se desloca com velocidade de 0,200 m/s para a direita (Figura).
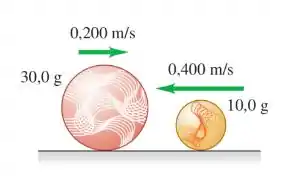
(a) Determine o módulo, a direção e o sentido de cada bola depois da colisão. (Como a colisão é frontal, todos os movimentos ocorrem ao longo da mesma linha.)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos mostra a colisão entre duas bolas de gude com diferentes massas e velocidades.
A questão nos pede para calcularmos o módulo, a direção e o sentido de cada bola depois da colisão.
Para isso, devemos utilizar o princípio da conservação do momento linear:
“O momento linear total de um sistema isolado permanece constante se nenhuma força externa atuar sobre ele.”
Em outras palavras, o momento antes da colisão é igual ao momento depois da colisão , ou seja:
E aí? Bora lá?
😉
Passo 2
Dessa forma, pela conservação do momento linear, temos:
Onde:
- e são as massas das bolas A e B, respectivamente;
- e são as velocidades iniciais das bolas A e B, respectivamente;
- e são as velocidades finais das bolas A e B, respectivamente.
Assim, substituindo os valores, temos:
Passo 3
Deixa eu te dizer uma coisa... quando temos uma colisão retilínea e elástica entre dois corpos, a velocidade relativa antes da colisão é igual e contrária a velocidade relativa após a colisão, ou seja:
Assim, substituindo os valores, temos:
Assim, temos o nosso sistema de equação:
Resolvendo nossos sisteminha, encontramos:
O sentido da primeira bola de gude é para esquerda (sinal negativo) e a segunda, para direita.
Entendeu direitinho? Responde aee ;)
