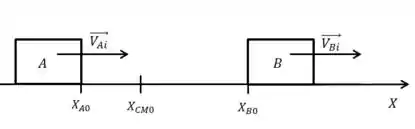
A figura mostra os blocos e que estão sobre uma superfície horizontal sem atrito. Use os dados do quadro do lado onde são respectivamente as posições dos blocos e do centro de massa do sistema. No instante ilustrado(, são respectivamente as velocidades imediatamente antes da colisão dos corpos . Considerando a colisão entre os blocos unidimensional, determine:

Dados:

1. O momento linear do sistema imediatamente após a colisão.
2. A velocidade do centro de massa do sistema.
3. O impulso do bloco transmitido pelo bloco sabendo que a velocidade imediatamente após a colisão de é igual a metade da velocidade imediatamente após a colisão de

a)

Beleza, agora podemos calcular a quantidade de movimento após a colisão. Mas se liga: Numa colisão, não existe variação de momento linear, não é mesmo? Então, podemos calcular o momento linear imediatamente antes da colisão:

E :

Não se esqueça de colocar o vetor unitário!

b)

Basta a gente usar a fórmula:

c)

Vamos fazer de (velocidade após a colisão)a nossa incógnita. Assim:

Como o momento se conserva:

Assim:

Bom, como o impulso é igual à variação de momento linear de um dos móveis, podemos escrever para

Pronto!