PARTE I
Uma bola de massa se move no sentido positivo do eixo x em um plano horizontal sem atrito com velocidade de valor . Ela colide com uma bola de massa em repouso. Após esse fato a bola passa a se mover com velocidade escalar no sentido negativo do eixo y. Desconhece-se se a colisão é elástica.
(a ) Obtenha o valor do ângulo que a velocidade final da bola A faz com o eixo x.
(b ) Encontre uma expressão literal para a velocidade escalar final da bola A em função de
PARTE II:
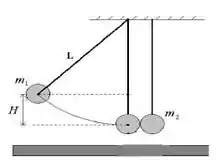
Um pêndulo em forma de bola com massa é largado de uma altura , conforme a figura ao lado, para colidir com outro pêndulo em repouso, constituído pela bola de massa . A colisão é frontal na direção horizontal de seus centros de massa e ocorre quando os dois estão na vertical. Pode-se desprezar a resistência do ar sobre os pêndulos durante a colisão.
Coloque Verdadeiro (V) ou Falso (F) nas afirmações abaixo e as justifique com base em leis físicas.
1- A força resultante externa durante a colisão é nula sobre o sistema de dois pêndulos e o momento linear é conservado.
2- A componente horizontal do Momento linear do sistema se conserva durante a colisão.
Passo 1
Calcularemos o valor do ângulo que a velocidade final da bola A faz com o eixo x
De acordo com o descrito no enunciado, temos os seguintes cenários:
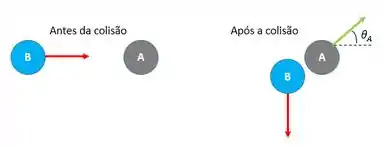
Como a resultante das forças externas é nula, podemos conservar o momento linear para o sistema. Assim, para cada um dos eixos (x e y), teremos:
No eixo x, teremos:
No eixo y, teremos:
Fazendo a divisão de por , teremos:
Logo,
Passo 2
Encontraremos uma expressão literal para a velocidade escalar final da bola A em função de
Isolando na equação , teremos:
Substituindo o valor de (encontrado no intem anterior) na equação , teremos:
Passo 3
Parte II
Analisando as afirmativas:
1 – Falso – Pois no momento da colisão a bola 1 possui força centrípeta atuando sobre ela e a bola 2 está em repouso, logo, a força externa resultante do sistema não é nula e por esta razão não podemos conservar o momento linear do sistema.
2 – Verdadeiro – No momento do choque não há forças externas horizontais atuando sobre as bolas. Como a lei de conservação do momento linear de um sistema é vetorial, podemos conservar a momento linear no eixo horizontal, mesmo tendo a força centrípeta atuando na bola 1 no eixo vertical.