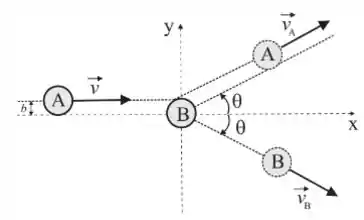
Um corpo de massa m incide com velocidade v sobre um outro corpo igual, com um parâmetro de colisão b, como mostrado na figura. Após a colisão, os dois corpos se afastam, formando um ângulo 2θ. Para , o módulo da variação da energia cinética de translação (∆T), em função da energia cinética inicial e do ângulo θ vale:

Bom, ele nos pediu a variação da Energia Cinética, e a gente já sabe calcular essa energia, sendo né? Mas a gente tem uma colisão, então pra gente descobrir essa velocidade envolvida na energia cinética a gente pode usar a conservação de momento linear, que é calculada por , lembra? Então vamo nessa: Antes a gente tem a partcila A se movendo com um momento linear de (no eixo x), que vai colidir com o corpo b, e logo após isso, vamos ter agora dois corpos em movimento! Mas como eles seguiram uma direção na diagonal e estamos tratando disso apenas no eixo x, temos que multiplicar nossa velocidae pelo pra encontrarmos sua componente no eixo x, sacou? Então a gente fica com um momento de . Pela conservação, o momento antes deve ser igual ao momento depois! Então:

E em Y nós vamos ter duas componentes, uma de e outra de , de módulo igual a ! Ou seja, !