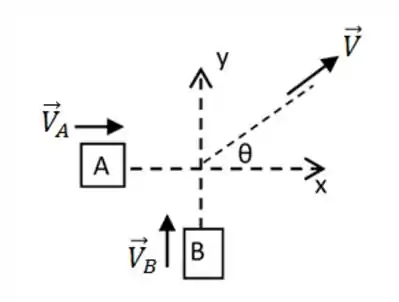
Dois automóveis viajam em duas estradas perpendiculares entre si, colidem e ficam juntos após a colisão. O carro tem massa de e tinha velocidade de antes da colisão. O carro tem massa de . As marcas de derrapagem dos carros juntos, imediatamente após a colisão fazem um ângulo de com a direção inicial do carro . Qual era a velocidade do carro antes da colisão?
Passo 1
Esse é um problema de conservação de momento linear em duas direções, e a primeira coisa que a gente tem que fazer é pensar no que acontece antes e no que acontece depois da colisão, anotando cada dado.
Após isso vamos aplicar a conservação do momento linear, podemos fazer vetorialmente que o momento linear inicial é igual ao final.
Ou separando por eixos.
Esse segundo jeito é mais fácil de visualizar um pouco, vamos fazer assim tá? Lembrando que:
Passo 2
Vamos analisar o que acontece antes da colisão: O carro tem massa e anda para a direita, ou sentido positivo de com velocidade . Já o carro possui massa e velocidade que queremos descobrir indicada no sentido positivo de , ou seja, pra cima . Se liga aí no desenho:
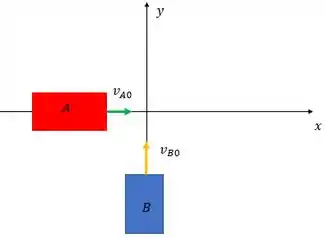
Sendo assim o momento linear desse sistema antes da colisão é em cada eixo:
Repara que o carro não tem momento linear na horizontal e o carro não tem momento linear na vertical, isso aí acontece por quê a velocidade desses carros nesses eixos é 0.
Vamos partir pra analisar o que acontece depois da colisão, ok?
Passo 3
Depois da colisão temos a seguinte situação: os carros e formam um sistema que anda junto, sendo assim a massa desse sistema é:
Esse sistema anda com velocidade final que não conhecemos e essa velocidade está angulada de em relação ao eixo. Se liga nesse desenho aí, pra gente entender legal:
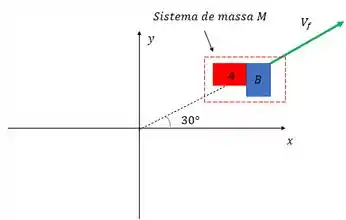
E aqui vai o bizu da questão, essa velocidade final deve ser decomposta nos dois eixos pra gente poder analisar separado cada momento linear. Podemos decompor ela da seguinte forma:
Então temos pros casos finais os seguintes momentos lineares:
E para o eixo :
Bacana, nosso próximo passo será aplicar a conservação do momento linear para cada eixo.
Passo 4
Vamos então aplicar essa conservação do momento linear, mas aqui precisaremos seguir uma lógica. Temos duas incógnitas e , vamos primeiro precisar encontrar e o jeito é começar analisando a conservação no eixo .
E aqui é substituir os valores que encontramos para cada um desses momentos lineares:
Isolando temos:
Bacana né, agora é só fazer isso pro outro eixo substituindo o valor de
Ufa, encontramos essa velocidade! Mais um exercício resolvido 😊.
Resposta