Enunciado das questões (Q4) e (Q5).
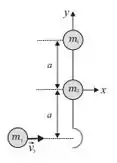
O sistema representado ao lado, formado por duas partículas de massas e , ligadas por uma haste em forma de gancho, de massa desprezível e comprimento , pode deslizar sem atrito sobre o plano horizontal . Uma terceira partícula, de massa , movendo-se sobre o plano com velocidade , colide com o sistema formado pelas partículas e , inicialmente parado, ficando presa no gancho.
(Q4) [1,0 ponto] A velocidade de translação do sistema depois da colisão é:
Passo 1
POW! Temos aqui um sistema com massas e uma colisão. E queremos justamente encontrar a velocidade final, ou seja, depois da colisão da partícula com a haste. O que você acha que podemos usar aqui?
Podemos usar as teorias da CONSERVAÇÃO DO MOMENTO LINEAR!
Essa teoria nos fala o seguinte: em um sistema sem ação de forças externas, o momento linear se conserva (antes e depois da colisão)...
Tá! Mas quem são esses momentos e como eles se relacionam com a velocidade que queremos determinar?
Passo 2
AHA! Respondendo essa pergunta é a grande beleza desse problema!
O momento linear é definido como . Antes de o sistema colidir, tínhamos duas partículas juntas em uma haste com uma velocidade (elas estavam paradas) e tínhamos uma partícula com velocidade . O momento linear então do sistema antes da colisão será...
Como a velocidade , e ...
Passo 3
Por outro lado, considerando agora a colisão, as três partículas vão estar juntas e com velocidade de centro de massa finais iguais (devido ao fato de estarem juntas e shallow now). Assim...
Onde ...
Então, como a quantidade de movimento linear se conserva...
Resposta
Letra C.