UFABC – Fenômenos Mecânicos – Lista 5 – Questão 02
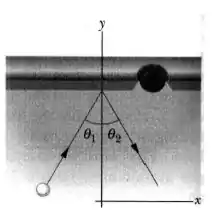
A figura abaixo dá uma vista superior da trajetória de uma bola de bilhar de quando ela bate na borda de uma mesa. O módulo da velocidade inicial é e o ângulo é . A rebatida inverte a componente da velocidade da bola, mas não altera a componente . Determine
(a) o ângulo e
(b) a variação do momento linear da bola em termos dos vetores unitários. (O fato de que a bola está rolando é irrelevante para a solução do problema.)
Passo 1
Oi, galerinha! Tudo bom? Essa questão parece complicada, mas vou facilitar para você!
Letra (a):
A grande sacada aqui é perceber que como a força da mesa sobre a bola aponta apenas na direção , então podemos afirmar que a componente do momento linear é conservada.
Beleza?
Além disso, devemos perceber que o enunciado diz que a componente da velocidade é invertida, portanto, o módulo da velocidade antes e depois é igual. Assim:
Repara que o ângulo é com o eixo , por isso temos uma relação de seno com o eixo (cateto oposto).
Simplicando a equação, ficamos com:
Portanto:
Beleza? Vamos para letra (b)?
Passo 2
Letra (b):
A variação do momento linear é a diferença do momento depois e antes. O momento linear em termos das componentes é:
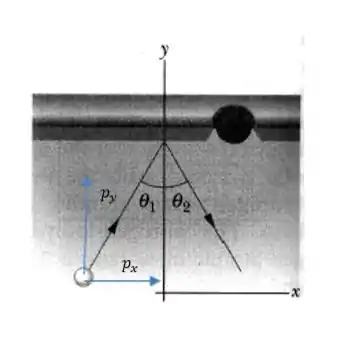
Daí a variação é:
Como a componente do momento linear é conservada e vimos que , então:
Substituindo os valores:
Beleza? E é isso!
Espero ter ajudado!
Resposta
- ;
- .