Um corpo de massa , movendo-se no sentido positivo X a uma rapidez , se rompe em duas partes cujas massas são , como é mostrado na figura.
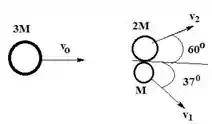
As velocidades escalares finais das partes em função de são, respectivamente,
(A)
(B)
(C)
(D)
(E)
Passo 1
Fazendo a conservação da quantidade de movimento no eixo X
Fazendo a conservação da quantidade de movimento no eixo Y
Substituindo :
Substituindo :