Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Harmônico Amortecido

Ver Teoria
Exercício 2134567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768

Enunciado

Na Fig. 15-15 o bloco possui uma massa de 1,50   k g e a constante elástica é 8,00   N / m . A força de amortecimento é dada por - b ( d x / d t ) , onde b = 230   g / s . O bloco é puxado 12,0   c m para baixo e liberado. (a) Calcule o tempo necessário para que a amplitude das oscilações resultantes diminua para um terço do valor inicial. (b) Quantas oscilações o bloco realiza nesse intervalo de tempo?

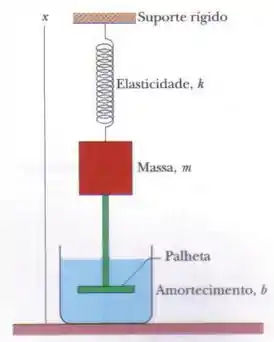
Passo 1

Bom, sabemos que somente a força de amortecimento é responsável por diminuir a amplitude do movimento. Vamos fazer a equação característica:

r 2 + b m r + k m = 0

E, calculando o ∆ :

∆   = 0,23 1,5 2 - 4   .   1   .   8 1,5 → ∆   =   - 21,3

Temos então um amortecimento subcrítico. O que podemos usar dessa informação? A equação geral! Isso mesmo!

x t = A e - γ t 2 cos ⁡ ( ω t + ϕ )

Onde A é a amplitude inicial do movimento e γ = b m

Passo 2

  1. O termo antes do cosseno A e - γ t 2 é a amplitude do movimento no momento t , portanto, o que queremos é:

    2. A t = A e - γ t 2 = 1 3 A

    Logo:

    - γ t 2 = ln ⁡ 1 3 → t = 2   l n 3 0,23 1,5

    t = 14,3   s

    Passo 3

  2. Sabemos que:

ω = ω 0 2 - γ 2 4 = k m - b 2 4 m 2

ω = 8 1,5 - 0,23 2 4   .   1,5 2 → ω = 2,31   r a d / s

Com a velocidade angular em mãos podemos obter o período!

ω = 2 π T → T = 2 π 2,31 → T = 2,72   s

E o número de revoluções é dado por:

n = t T = 14,3 2,72 → n = 5,27   r e v

Como n deve ser um número inteiro, podemos usar:

n ≅ 5   r e v

Resposta

  1. 14,3   s
  2. 5   r e v

Exercícios de Livros Relacionados

137. Uma máquina de 200k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅
138. Represente graficamente a resposta x do corpo de 20k g ao longo do intervalo de tempo 0 ≤ t ≤ 1 segundo. Determine os valores máximo e mínimo de x e seus respectivos instantes de tempo. As condiç
Para uma criança em um balanço, a amplitude cai em um fator de 1 e em cerca de oito períodos, se nenhuma energia mecânica adicional for fornecida ao sistema. Estime o fator Q para este sistema.
Para o cilindro do Prob. 8/8, determine o deslocamento vertical x, medido para baixo no sentido positivo em milímetros, a partir da posição de equilibro, em termos do tempo t, em segundos, medido a pa
Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?