Assinale a alternativa correta a respeito de um bloco preso a uma mola na presença de amortecimento e na ausência de quaisquer forças externas.
- Quanto maior o coeficiente de dissipação tanto mais rápido o sistema tende ao equilíbrio.
- A energia cinética do bloco decresce em todos os instantes de tempo.
- Para saber se o amortecimento é crítico, supercrítico ou subcrítico devemos analisar as condições iniciais.
- No regime subcrítico a posição ocupada pelo bloco pode ser um número imaginário.
- A energia mecânica do bloco não cresce em todos os instantes de tempo.
Passo 1
Vamos analisar uma por uma:
a): Errada: Aqui entra aquela classificação em subcrítico, crítico, e supercrítico. Vamos lembrar? É assim:
Quando : amortecimento subcrítico;
E:
Quando : amortecimento crítico;
E:
Quando : amortecimento supercrítico;
E:
E o é o coeficiente de dissipação classificação, a gente pode notar que o regime com maior coeficiente é o supercrítico.
Mas no nosso capítulo a gente viu que é o crítico que é o regime que chega mais rápido no equilíbrio, certo?
Então, é errada.
b): Errada: Essa afirmação tá tentando te confundir. Como existem forças de dissipação, o que acontece é que é a Energia Mecânica que decresce sempre, não a cinética.
E porque a energia cinética não decresce sempre? Bom, porque sempre que a velocidade aumenta, a energia cinética aumenta, já que a energia cinética é dada por:
Por exemplo, dê uma olhada no gráfico abaixo:
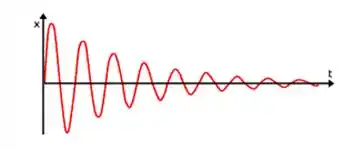
É o gráfico do amortecimento subcrítico. Como o gráfico é de , a derivada dá a velocidade:
E a derivada é o coeficiente da reta tangente à reta tangente ao gráfico, certo?
Então, quando a oscilação atinge um vale, a derivada dá zero...mas logo após isso, ela começa a crescer. Isso quer dizer que a velocidade começa a crescer e, então, a energia cinética também começa a crescer.
Resumindo: Toda vez que que a velocidade cresce a energia cinética cresce, e a velocidade em um MHA, como no do exemplo, costuma oscilar. Então ela não só decresce o tempo todo.
Passo 2
c): Errada:
Não não, devemos analisar é a relação entre e
Quando : amortecimento subcrítico;
E:
Quando : amortecimento crítico;
E:
Quando : amortecimento supercrítico;
E:
d): Errada:
A função do MHA pra um regime subcrítico é essa aqui:
Não há componentes imaginários nisso. Então, a função sempre retorna valores Reais.
Passo 3
e):Correta:
Na verdade, como a energia mecânica é dada por:
E a amplitude inicial decai a partir daquele fator que tem em todas as formulas de todos os regimes:
Ou seja:
Então, a energia mecânica sempre decai! Ela não cresce!
Resposta
e)