Um canhão de massa possui um sistema de recuo, que é formado por uma mola de constante elástica e um amortecedor com coeficiente de amortecimento . No instante , o canhão dispara um projétil de massa com uma velocidade.
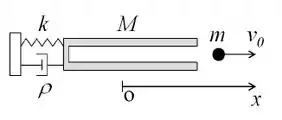
(a) Calcule a velocidade do tambor do canhão no momento do disparo?
(b) Determine o tipo de amortecimento (subcrítico, supercrítico ou crítico)? Justifique sua resposta.
(c) Considerando que no instante t = 0 s, o tambor do canhão se encontra na posição x = 0 m, determine a posição em função do tempo x(t) do tambor do canhão.
(d) Determine o tempo que leva para o tambor do canhão atingir o menor valor de x?
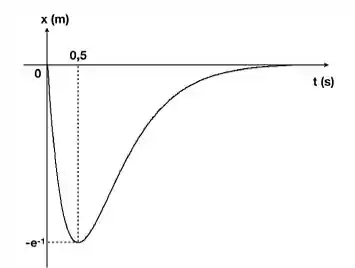
(e) Esboce o gráfico de x(t), indicando possíveis extremos dessa função.
Passo 1
A) Por conservação do momento linear do sistema “canhão+projétil”, temos ao longo do eixo do canhão e, portanto
Passo 2
B) A classificação do regime de amortecimento segue os critérios
As constantes nesse caso são:
Portanto, o regime de amortecimento é crítico
Passo 3
C) A solução geral para a posição do tambor do canhão no regime de amortecimento crítico é dada por
de forma que, derivando-se a expressão acima com respeito ao tempo, a velocidade do tambor é
e as condições iniciais para o problema em questão
A solução final é
(t em segundos)
Passo 4
D) O instante em que atinge seu mínimo valor deve corresponder também ao momento em que a velocidade se anula
A derivada segunda (aceleração) é positiva em , logo, trata-se de um mínimo de
Passo 5
E) A função tem uma derivada negativa em
um mínimo em
e vai a zero por valores negativos para tempos grandes
Resposta
A)
B) crítico
C)
D)