Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Harmônico Amortecido

Ver Teoria
Exercício 3412345678910111213141516171819202122232425262728293031323335363738394041424344454647484950515253545556575859606162636465666768

Enunciado

UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 11d

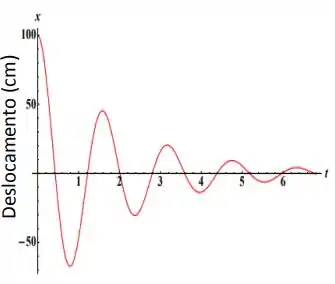
O gráfico ao lado representa o movimento de um oscilador harmônico amortecido.

d ) Escreva a equação para o oscilador amortecido.

Passo 1

Oiie, tudo bem?

O enunciado nos dá o seguinte gráfico

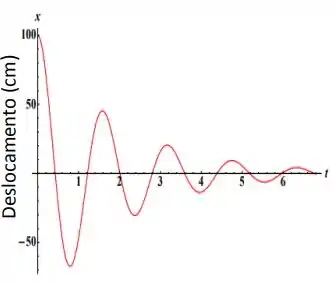
este gráfico representa um oscilador harmônico amortecido! Estas oscilações são regidas pela equação

x ( t ) = A e β t c o s ( ω 1 t )

em que

ω 1 = | β 2 - ω 0 2 |

com

β = - b 2 m e ω 0 2 = k m

Esta alternativa nos pede

d ) Escreva a equação para o oscilador amortecido.

Nas alternativas anteriores estimamos que

ω 1 ≈ 4,49   r a d   s - 1 e | β | ≈ 0,77

e, obtivemos uma frequência natural da forma

ω 0 ≈ 4,42   r a d   s - 1

Agora, precisamos apenas juntar todos os dados e escrever a nossa solução! Saca só!

Passo 2

Temos que em t = 0 temos um pico em x = 100 , portanto, esta será nossa amplitude, e contanto que usemos o formato de cosseno a fase é nula, a frequência é a frequência ω 1 , portanto, a equação é dada por

x ( t ) = 100 e - 0,77 t c o s ( 4,49   t )

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

x ( t ) = 100 e - 0,77 t c o s ( 4,49   t )

Exercícios de Livros Relacionados

137. Uma máquina de 200k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅
138. Represente graficamente a resposta x do corpo de 20k g ao longo do intervalo de tempo 0 ≤ t ≤ 1 segundo. Determine os valores máximo e mínimo de x e seus respectivos instantes de tempo. As condiç
Para uma criança em um balanço, a amplitude cai em um fator de 1 e em cerca de oito períodos, se nenhuma energia mecânica adicional for fornecida ao sistema. Estime o fator Q para este sistema.
Para o cilindro do Prob. 8/8, determine o deslocamento vertical x, medido para baixo no sentido positivo em milímetros, a partir da posição de equilibro, em termos do tempo t, em segundos, medido a pa
Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?