Um objeto de massa é preso a uma mola de constante elástica . O sistema, que está sujeito à ação de uma força de amortecimento , é colocado para oscilar.
Sabendo que esse oscilador harmônico amortecido tem fator de qualidade , e sua equação de movimento é dada por , determine:
- A solução da equação de movimento sabendo que e que a constante de fase é
- Qual é o tempo necessário para que a amplitude do movimento se reduza à metade do seu valor?
- Esboce um gráfico do valor médio da energia como função do tempo para uma massa . Deixe claro as unidades adotadas
Se necessário use
Passo 1
Temos que olhando a equação de movimento do objeto podemos identificar a frequência
Temos então
Passo 2
Pelo fator de qualidade podemos descobrir o
Como o critério
é obedecido, temos um amortecimento sub-crítico.
Passo 3
A solução geral é dada por
Com
Já a velocidade desse objeto é dada por
A condição inicial para a velocidade
E que
Como e , temos
Passo 4
Assim juntando tudo temos
Passo 5
Temos que a amplitude desse momento varia no tempo como
Para que a amplitude caia a metade temos que
Passo 6
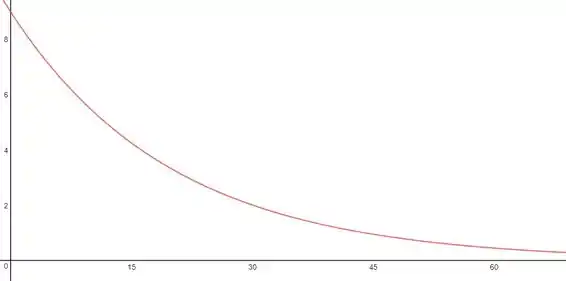
No regime subcrítico a energia média decai exponencialmente no tempo
A energia média inicial pode ser dada pela energia inicial
A posição inicial é dada por
E a velocidade inicial é dada por (o enunciado já disse!!!)
Assim
Assim
(Energia em Joule)
E o esboço do gráfico fica mais ou menos assim
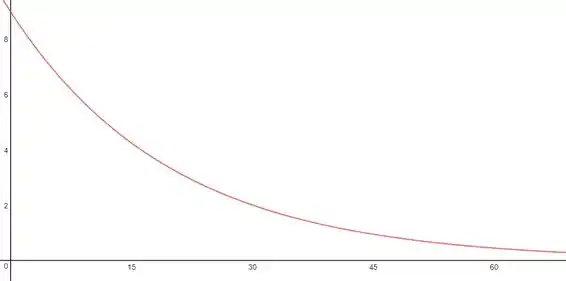
Resposta
- Gráfico de decaimento exponencial