UFMG, Sem Campus, UFMG - Problemas sobre Oscilador Harmônico, Questão 13d
A figura ao lado mostra o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola. Usando as informações constantes do gráfico determine:
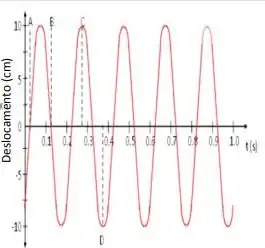
d. Calcule a velocidade máxima.
Passo 1
Eaew, belezinha?
O enunciado nos pede para determinar a velocidade máxima dado o movimento de um corpo, de massa m = 2,00 kg, sobre uma superfície horizontal lisa e preso à uma mola usando as informações do gráfico:
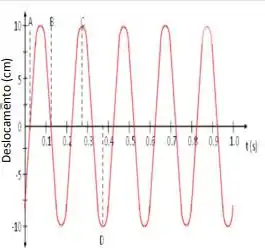
Então vamos lá!
Passo 2
Temos que a velocidade é a derivada da posição com relação ao tempo, sendo
Então,
Passo 3
Temos então que a velocidade será máxima quando , assim
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Exercícios de Livros Relacionados
137. Uma máquina de 200k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅
138. Represente graficamente a resposta x do corpo de 20k g ao longo do intervalo de tempo 0 ≤ t ≤ 1 segundo. Determine os valores máximo e mínimo de x e seus respectivos instantes de tempo. As condiç
Para uma criança em um balanço, a amplitude cai em um fator de 1 e em cerca de oito períodos, se nenhuma energia mecânica adicional for fornecida ao sistema. Estime o fator Q para este sistema.
Para o cilindro do Prob. 8/8, determine o deslocamento vertical x, medido para baixo no sentido positivo em milímetros, a partir da posição de equilibro, em termos do tempo t, em segundos, medido a pa
Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?