Um objeto de massa m está preso a uma mola ideal de constante elástica e se move no eixo . Ele também está sujeito a uma força de amortecimento proporcional à velocidade , onde é uma constante positiva. Sobre este sistema, são feitas as seguintes afirmativas:

I. Se , há oscilações.

II. Se , o regime de amortecimento é supercrítico.

III. Como se trata de um oscilador amortecido é sempre decrescente, independente das condições iniciais.

São verdadeiras:

(a) Somente I e II.

(b) Somente II.

(c) Somente II e III.

(d) Somente I.

(e) Somente III.

(f) Somente I e III.

(g) Todas.

(h) Nenhuma.

II. Se , o regime de amortecimento é supercrítico.

Para amortecimento supercrítico devemos ter:

Então:

Então também é verdadeira.

III. Como se trata de um oscilador amortecido é sempre decrescente, independente das condições iniciais.

Ok, aqui como ele tá falando de função decrescente, nós temos que pensar na derivada. Quando a função é decrescente, a derivada é negativa. Quando é crescente, a derivada é positiva. E y(t) é função do MHA! Vamos lembrar dos gráficos:

Subcrítico

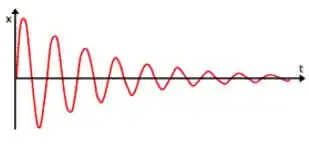
Crítico

Supercritico

Todos esses gráficos tendem pra zero depois de um tempo. Mas todos eles também têm uma parte crescente, de derivada positiva (é só você pensar na reta tangente à curva). Então tem uma parte crescente, e o mesmo vai valer pro módulo! Então a afirmativa é errada.

Alternativa correta: Apenas I e II estão certos.