Um pêndulo simples, em seu laboratório de física, é composto por um fio de comprimento e uma bolinha (pontual) de massa presa à sua ponta. Para iniciar o balanço da bolinha, você coloca um ventilador próximo à ela, soprando uma corrente horizontal de ar de velocidade escalar , resultando em uma força (como mostrado abaixo). Enquanto o ventilador está ligado, o sistema fica em equilíbrio, com um ângulo com a vertical, com .
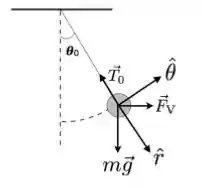
Obtenha o módulo do vetor para valores gerais de , em termos do ângulo , de e de .
Você desliga o ventilador e deixa que o pêndulo oscile. Supondo que a força de arrasto do ar seja da forma , sendo uma constante e a velocidade da bolinha, deduza a equação diferencial exata que descreve o deslocamento angular do pêndulo para , justificando de forma sucinta os termos usados na equação.
Considere o regime de pequenas oscilações, onde. Dadas as condições iniciais do problema, obtenha a função exata para .
Determine a constante de decaimento deste pêndulo.
Quanto tempo levará para a amplitude de oscilação do pêndulo chegar a um valor ?
Nota: dê suas respostas em termos dos parâmetros do problema:
Passo 1
Temos o pendulo em repouso (, ou seja, temos equilíbrio de forças, vamos então decompor em e .
Como temos equilíbrio de forças
Como o ângulo está entre e , como vemos na figura
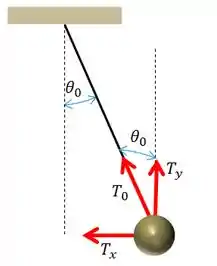
Assim,
E agora podemos usar a relação de
Então
Para ângulos pequenos isso quer dizer podemos assumir que .
Então chegamos em termos gerais que
Passo 2
Quando tirarmos o ventilador o pendulo sairá do repouso, onde formava um ângulo com a vertical, e entrará em um movimento oscilatório, porém mesmo em movimento as forças e continuaram agindo no pendulo, sendo assim vamos adotar a origem do eixo cartesiano no teto com o fio.
Começando pela equação da posição, temos que
Agora, vamos escrever as equações do movimento nas coordenadas e , pois temos que
Assim, temos que
Ainda, podemos escrever a equação da velocidade do movimento, pois temos que
Sabemos que o ângulo está variando com o tempo, assim derivando a equação da posição temos
Escrevendo em coordenadas polares temos
E do mesmo jeito que fizemos faremos para descobrir a equação da aceleração
Lembrando da regra da cadeia de derivadas, temos que
Temos que a derivada do vetor é dada por:
Assim a equação da aceleração é
Passo 3
Bem, agora que descobrirmos a equação da aceleração, podemos relaciona-la com as forças no problema, certo?
Pela segunda lei de Newton, temos que , vamos usar essa lei!
As forças que temos são ( que esta na direção radial), (que é função da velocidade, que já encontramos) e (que está na direção , e por isso vamos decompor em e )
Nossas forças são:
Como a tensão só tem componente na direção de e não sabemos o valor de , então vamos usar apenas a componente para descobrirmos a equação do movimento.
Assim, em temos
Reescrevendo essa equação temos
Podemos dividir ambos os lados por
Assim, chamamos de
E então chegamos em
Passo 4
Para o regime de pequenas oscilações temos que . Assim a equação pode ser reescrita como:
Encontramos a equação diferencial que representa um movimento harmônico amortecido, e sabemos que a força de arrasto tende a parar o movimento do pendulo, mas ela é uma força muito pequena ( tanto que geralmente desprezamos essa força), assim, temos o nosso sistema em amortecimento subcrítico. Ele irá oscilar muito antes de parar definitivamente, certo?
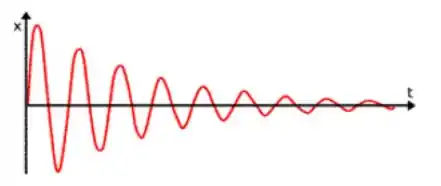
Então sabemos que a nossa solução será do tipo:
Temos que , então falta apenas determinamos a amplitude e a fase do movimento. Para isso vamos usar os dados de contorno do sistema.
Pela primeira situação de contorno temos:
A segunda condição de contorno, nos fornece que
Temos que
Como vimos que a força de arrasto é muito pequena temos que é pequeno o suficiente para consideramos que
Assim,
Substituindo o valor de , Bem novamente para simplificar vamos usar o fato de ser muito menor que , assim
Chegamos em
Agora se voltarmos na equação que tínhamos encontrado
E substituirmos esse valor de seno, encontraremos
Assim
Voltando na outra condição de contorno
Descobrimos que
Assim,
Pois, temos que
Como
e
Passo 5
a constante de decaimento é dada por
Porém não conhecemos a constante , para isso, vamos analisar o instante antes em que com o ventilador ligado o pendulo entrou em repouso.
Pois nesse momento temos , pois o pendulo entrou em repouso, e para isso alguma força teve que anular a força do vento e foi o arrasto. Assim
Já calculamos o valor da força do vento no passo 1, então temos que
Como a velocidade gerada pelo vento do ventilador tem módulo , então sabemos que a força de arrasto será dada por
Assim temos que
Voltando para a equação do decaimento, chegamos em
Consideramos pequenos ângulos, ainda podemos escrever
Passo 6
A amplitude de oscilação é
Assim, para chegar em
Fazendo dos dois lados, temos
Assim,
Lembre-se que para chegarmos até aqui consideramos que a força de arrasto é muito pequena e que por isso