UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 11a
O gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
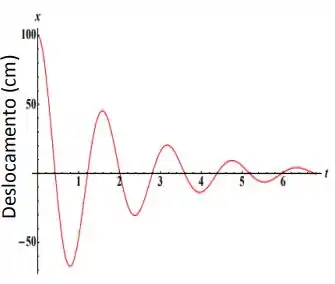
Usando as informações do gráfico faça uma estimativa dos valores da frequência de oscilação e do coeficiente de amortecimento .
(Dica: se necessário amplie a figura)
Passo 1
Oiie, tudo bem?
O enunciado nos dá o seguinte gráfico
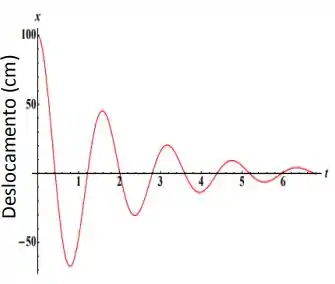
este gráfico representa um oscilador harmônico amortecido! Estas oscilações são regidas pela equação
em que
com
e
Esta alternativa nos pede
Usando as informações do gráfico faça uma estimativa dos valores da frequência de oscilação e do coeficiente de amortecimento .
Vamos tentar usar as informações acima para estimar o que foi pedido! Vem comigo!
Passo 2
Primeiro, temos que a frequência está relacionada ao período pela relação
e é o tempo entre dois picos em nosso gráfico. Ou seja, aproximadamente
de forma que
Agora, para encontrarmos a constante vamos lembrar um pouco do conceito de meia-vida no decaimento exponencial!
Passo 3
Para esta estimativa em específico vamos lembrar o papel da exponencial neste problema! Temos um decaimento exponencial, ou seja, o argumento da exponencial está relacionado a uma grandeza com unidade temporal chamada tempo de “meia-vida”, que é quando a amplitude da oscilação cai pela metade do que era originalmente! O argumento da exponencial e o tempo de meia vida estão relacionados pela relação
Observando a figura note que a amplitude cai abaixo da metade em uma oscilação completa, mas apenas um pouco abaixo da metade, portanto, temos que é um pouco menor que um período, vamos tomar como aproximadamente , sendo assim, temos que
A primeira alternativa foi isso! Vamos para a próxima!
Resposta
e