Duas balanças são constituídas, cada uma, por uma mola e um prato, em que se deposita uma massa a ser medida. Observa-se que para a primeira balança, o prato não oscila, mas a balança demora um certo tempo para marcar o valor correto depois que a massa é posta no prato. Nota-se também que a segunda balança oscila várias vezes antes que o prato pare e esse valor possa ser lido. Assinale a alternativa INCORRETA:
(a) Na primeira balança observa-se um regime de amortecimento crítico ou supercrítico.
(b) Na segunda balança observa-se um regime de amortecimento subcrítico.
(c) Quanto mais amortecido o sistema, menos tempo a balança leva para marcar o valor correto.
(d) Se não houvesse nenhum tipo de amortecimento, a balança poderia oscilar por tempo indeterminado.
(e) O valor da massa altera a frequência natural de oscilação do sistema massa+prato+mola.
Passo 1
No movimento harmônico amortecido,
Que tem equação característica:
Onde
Pode possuir três soluções diferentes:
Para , amortecimento supercrítico:

Para , amortecimento crítico, onde o decaimento é mais rápido do que no supercrítico:

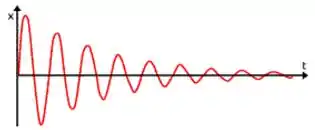
Para amortecimento subcrítico, onde o sistema decai com um movimento oscilatório.
Passo 2
Na primeira balança, o prato não oscila, logo o movimento não pode ser subcrítico.
Já a segunda balança oscila várias vezes antes de parar, logo o movimento é obrigatoriamente subcrítico.
Logo, as alternativas a e b estão corretas.
Passo 3
A frequência natural de oscilação do sistema é
Logo, a alternativa e está correta, ela depende da massa.
Passo 4
Vamos analisar as duas últimas alternativas:
(d) Se não houvesse nenhum tipo de amortecimento, a balança poderia oscilar por tempo indeterminado.
Se não tem amortecimento , então a equação seria
Cuja solução é uma oscilação não-amortecida do tipo
Alternativa correta.
Passo 5
E por último,
(c) Quanto mais amortecido o sistema, menos tempo a balança leva para marcar o valor correto.
Podemos ver que o caso que leva menos tempo para marcar o valor correto é o amortecimento crítico, .
Mas no caso supercrítico, a balança demora mais tempo, e
Ou seja, o amortecimento () é maior mas a balança demora mais tempo para chegar no equilíbrio. Alternativa incorreta!
Resposta
(c) Quanto mais amortecido o sistema, menos tempo a balança leva para marcar o valor correto.