O gráfico ao lado representa o movimento de um oscilador harmônico amortecido.
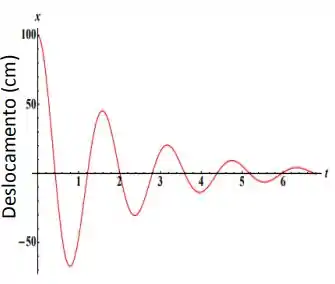
Determine a frequência natural do MHS.
Passo 1
Oiie, tudo bem?
O enunciado nos dá o seguinte gráfico
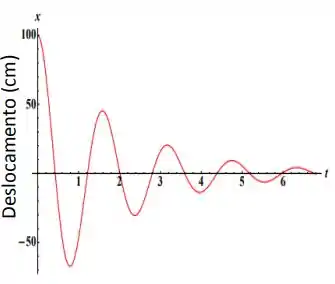
este gráfico representa um oscilador harmônico amortecido! Estas oscilações são regidas pela equação
em que
com
e
Esta alternativa nos pede
Determine a frequência natural do MHS.
Nas alternativas anteriores estimamos que
e
Vamos usar esses valores para encontrar a nossa frequência natural! A dica já está acima! Bora lá!
Passo 2
A frequência natural é , portanto, usando a definição que apresentei no passo 1, temos que
elevando os dois lados ao quadrado, temos que
usando que
temos que
ou seja, para obtermos uma real, precisamos que
ou simplesmente
Mais uma alternativa já era! Te vejo na próxima!