Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução a Ondas

Ver Teoria
Exercício 571234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

A figura abaixo mostra o perfil y ( x ;   0 ) de uma onda transversal que se propaga com velocidade v   =   3   m / s   no sentido crescente de x .

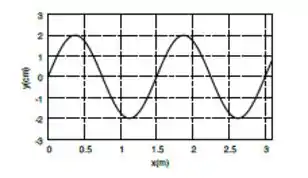
  1. Qual o comprimento de onda desta onda?
  2. Qual o período das oscilações de um dado ponto?
  3. Usando a forma de função de onda y ( x ;   t )   =   A c o s ( k x - ω t + δ ), com A   >   0 , para descrever esta onda, determine A k ,   ω   e   δ .(Dica: Pelo gráfico vê-se que a velocidade do ponto na origem x = 0 é negativa em t = 0 .)
  4. Qual a velocidade máxima atingida por um ponto qualquer?

Justifique suas respostas.

Passo 1

Galera, para resolver esta questão basta simplesmente analisar o gráfico. Vemos no gráfico que, partindo do zero, em x = 1 ,   5 m a função começa a se repetir. Portanto λ = 1 ,   5   m .

Passo 2

Bom, como sabemos lá da teoria de ondas que a velocidade da onda é dada por:

v = λ f = λ T

Rearranjando a equação para descobrir nossa variável independente T , temos:

T = λ v = 1,5 3 = 0,5 s

Passo 3

Vemos do gráfico que o deslocamento máximo de qualquer ponto a partir do equilíbrio vale 2 ,   0   c m . Portanto esta é a amplitude A .

Como a função se repete espacialmente a intervalos, λ ,

K x + λ = K x + 2 π

logo:

    K = 2 π λ = 2 π 3 2 = 4 π 3   r a d / m .

Analogamente, o movimento de um dado ponto se repete a intervalos de tempo T,

ω t + T = ω t + 2 π

Sendo,

ω = 2 π T = 2 π 0,5 = 4 π r a d s

As condições iniciais são y 0,0 = 0 , ∂ y ∂ t 0,0 < 0 , logo:

A c o s δ = 0

δ ± π 2

Derivando a função de onda dada pelo enunciado, temos:

∂ y ∂ t = - ω A ( - s e n ( k x - ω t + δ )

A nossa condição nos diz que ∂ y ∂ t 0,0 < 0 , aplicamos então a condição na nossa função derivada:

∂ y ∂ t 0,0 = A ω s e n   δ < 0

∴

δ = - π 2

Portanto a onda é descrita por:

y x , t = 2 c m cos ⁡ 4 π 3   r a d / m x - 4 π   r a d / s t - π 2 .

Passo 4

A velocidade máxima atingida em um determinado ponto é dada por:

v y = ∂ y ∂ t = A ω s e n k x + ω t + δ

Então,

v y m a x = ω A = 4 π . 2 = 8 π c m / s

Resposta

A)   λ = 1 ,   5   m

B) T = 0,5 s

C) y x , t = 2 c m cos ⁡ 4 π 3   r a d / m x - 4 π   r a d / s t - π 2 .

D)   v y m a x = 8 π c m / s

Exercícios de Livros Relacionados

13.1. A corda de um piano emite um lá médio vibrando com uma frequência primaria igual a 220 Hz. a) Calcule o período e a frequência angular. b) Calcule a frequência angular de uma soprano emitindo um
Feixes de laser enviados para a Lua são um recurso rotineiro para se determinar com precisão a distância entre a Terra e a Lua. No entanto, para determinar a distancia com precisão, correções devem se
Use a equação de onda para determinar a velocidade de uma onda dada por y x , t = 3,00m m sen ⁡ [ 4,00m - 1 x - 7,00s - 1 t ] .
Se, no exemplo 15.3 você não desprezasse a massa da corda, qual seria a velocidade da ondaNa extremidade inferior da corda;No meio da corda;Na extremidade superior da corda?
Um oscilador harmônico simples em x = 0 gera uma onda em uma corda. O oscilador opera em uma frequência de 40 H z e com uma amplitude de 3 c m . A corda possui uma densidade linear de 50 g / c m e est