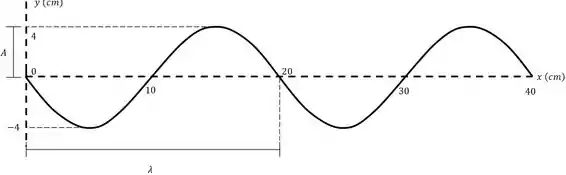
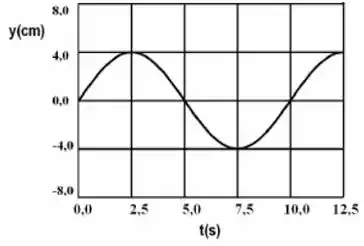
Uma onda senoidal transversal com está se propagando no sentido de crescente. O deslocamento da partícula em , a partir do equilíbrio e em função do tempo, é mostrado na figura.
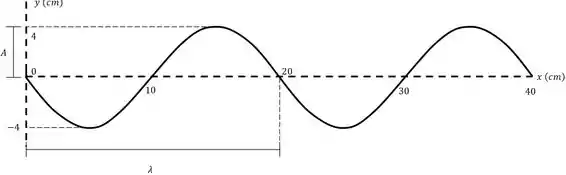
- Faça um esboço da onda no instante no trecho contido entre os pontos e . Indique claramente a amplitude, o comprimento de onda e o sinal da derivada em .
- Qual a velocidade de propagação da onda?
- Escreva a função que descreve a onda em qualquer e .
- Calcule a velocidade transversal da partícula em e
Passo 1
a)
Como ele quer a onda até vamos ter dois comprimentos de onda, lembrando que
A derivada que ele quer é
Lembrando que a equação da onda harmônica se deslocando para direita fica
onde:
Derivando isso em relação a vamos ter
Em , vamos ter
Não sabemos o sinal desse seno, o gráfico que temos pode nos dizer a derivada dessa função, porque vamos para a derivada em relação ao tempo? Olha como ela fica,
Pelo gráfico a função é crescente na origem e no inicio do movimento então a derivada é positiva
O que implica
Que nos faz concluir que
Isso nos diz que o gráfico inicialmente é decrescente, então a função fica
Passo 2
b)
Pelo desenho no enunciado conseguimos perceber que o período da onda vai ser
Dessa forma a frequência é
A velocidade de propagação então fica
Passo 3
c)
Já vimos que a equação da função vai ser
Temos que achar cada constante dessa fórmula
A amplitude já sabemos
Vamos achar e
Passo 4
Falta achar
Em sabemos o valor de
Então devemos ter a fase tal que
Como vimos ali no passo 1. Isso nos diz o valor desse angulo
A equação fica
Com em centímetros.
Passo 5
d)
A velocidade transversal nada mais é que a derivada no ponto que ele pediu.
Basta derivar em relação ao tempo a equação do passo
Basta agora colocar e
E o seno desse angulo vai ser
Resposta