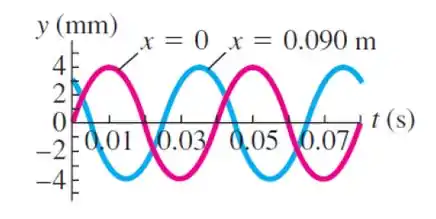
Uma onda senoidal é produzida numa corda que está esticada ao longo do eixo . O deslocamento da corda em função do tempo está representado na figura para partículas na posição e .
- Qual é a amplitude da onda?
- Qual é o período da onda?
- Escreva a equação da onda em função de e assumindo que a onda está se propagando no sentido . Use para o número de onda. Atenção para a fase! [Dica: use os pontos e para achar a fase.]
- Se os pontos m estão contidos em um intervalo de um comprimento de onda e assumindo que a onda se propaga no sentido , determine o comprimento de onda e a velocidade da onda.
Se necessário use
Passo 1
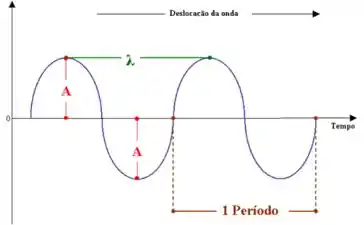
Sabemos que a amplitude é a distância no vértice de uma crista até a seguinte. Logo, do gráfico observamos que a amplitude é igual a .
Passo 2
O período é o tempo(t) de um ciclo completo de uma oscilação de uma onda. Do gráfico, observamos que o período é igual a 0.04 s.
Passo 3
A função de onda de uma onda senoidal de forma geral para uma onda se propagando em dada por:
Para achar a fase , podemos olhar para e consequentemente, .
Pegando outro ponto, , percebemos sen( logo .
Passo 4
Vamos olhar para o ponto .
Logo:
,
e o argumento da função é algo maior que dado que:
.
Assim e sendo:
A velocidade da onda será:
Resposta
a)
b)
c)
d)