UFMG, Sem Campus, UFMG - Problemas sobre Oscilador Harmônico, Questão 36f
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
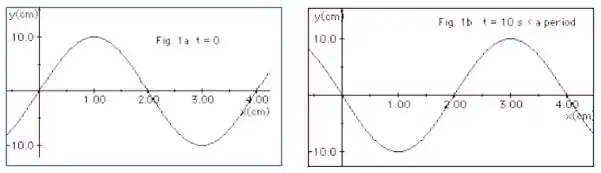
f. Desenhe, em um gráfico, o comportamento do deslocamento y em função do tempo para as posições x = 0, x = 2 cm e x = 4,0 cm, para o intervalo de t = 0 até t= 20 s.
Passo 1
Eaew, belezinha?
Temos que desenhar, em um gráfico, o comportamento do deslocamento y em função do tempo para as posições x = 0, x = 2 cm e x = 4,0 cm, para o intervalo de t = 0 até t= 20 s.
Então vamos lá!
Passo 2
Temos que uma função que descreve esse comportamento é dada por
sendo, o valor máximo de y, e temos que e . Assim, podemos escrever a função
.
Então para construir os gráficos basta fixar os valores de x solicitados.
Passo 3
Para , :
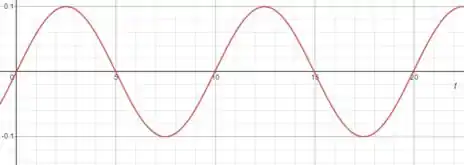
Passo 4
Para , :
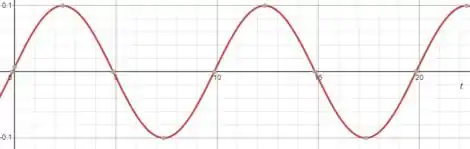
Passo 5
Para , :
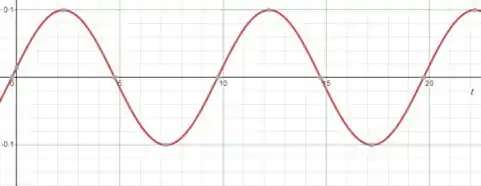
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.