UFF – Física III – P2 – 2022.1 – Q5
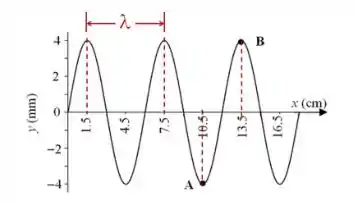
O deslocamento de uma corda vibrante em função da posição num certo instante é mostrado na figura. A onda viaja na direção positiva do eixo x com velocidade de 10 cm/s. A e B são dois pontos da corda. Determine (a) a frequência da onda e (b) a diferença de fase entre o ponto B e o potno A.
Passo 1
E aí, galerinha! Tudo na paz por aí?
Agora estamos no assunto de ondas de física \o/
Primeiro de tudo a gente tem que saber identificar o que o enunciado tá pedindo pra gente encontra, certo? Na letra (a) e (b) ele pede respectivamente a frequência da onda e a diferença de fase entre o ponto B e A.
A frequência de uma onda é dada por:
Onde e são o comprimento de onda e velocidade, que foram dados de forma direta e indireta no enunciado. A velocidade foi dita ser , enquanto que o comprimento de onda é a distância entre as duas cristas ou dois vales de uma onda.
Nesse caso:
Por sua vez, a diferença de fase é calculada por:
Onde
Com as nossas fórmulas na mão, agora, bora cair no braço com essa questão!!
Passo 2
Bem, dado a velocidade e calculado , a letra (a) pode ser calcuada, certo?
Agora que temos o valor de também podemos calcular o valor da diferença de fases:
Onde e representam as distâncias dos pontos e .
UHUUUULLL! Essa questão deu um sustinho no início, mas funcionou \o/