A figura abaixo apresenta a evolução temporal de um ponto, de uma onda senoidal propagando-se a no sentido positivo.
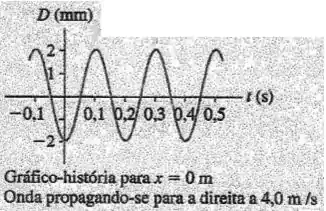
Qual o comprimento de onda correspondente?
Qual é a constante de fase de onda?
Escreva a equação para os deslocamentos produzidos no meio por essa onda (em função do tempo e do espaço)
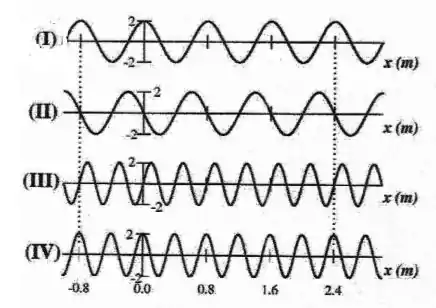
Qual das figuras ou abaixo, representa a imagem da onda para o instante
Passo 1
O comprimento de onda é calculado como:
é frequência e pode ser escrito como o inverso do período. é o período da onda e podemos descobir pelo gráfico, basta observarmos quanto tempo a onda gasta para se repetir.
A velocidade foi dada pelo enunciado, .
Então o comprimento de onda será:
Passo 2
Para descobrirmos a constante de fase primeiro temos que lembrar como é a função que descreve o movimento de uma onda.
Essa função é do tipo:
Não conhecemos nem nem , apenas conhecemos o valor da amplitude pelo gráfico e a fase é o que queremos. Então a ideia é zerarmos e , pois não os conhecemos. Para isso vamos estudar a função no ponto .
Vamos olhar no gráfico agora, quanto vale a função nesse ponto? Vale .
Então, chegamos que:
E para quais ângulos o seno é ?
Passo 3
Agora temos que escrever a equação da função de onda. No item anterior terminamos de escrever a função, mas não sabíamos os valores de nem de . Para esse item teremos que descobrir esses valores.
A constante da mola é dada por:
O comprimento de onda, , descobrimos no item e vale . Assim:
Já a frequência de oscilação é dada por:
Podemos escrever a frequência como inverso do período, pois este nós já sabemos .
A amplitude e a constante de fase nós já sabemos, então basta escrever a função de onda:
Passo 4
Agora nos foi dado gráficos representando uma onda nas coordenadas .
Então o primeiro passo é observar se o comprimento de onda está representado corretamente. O comprimento de onda da nossa onda é , então uma onda mede isso, o que significa que a onda só se repetirá após .
Por isso podemos eliminar as opções e já que nestas o comprimento de onda é menor, ou seja, a onda se repete antes de percorrer .
Agora vamos analisar a amplitude, que o que temos em comum nos dois gráficos, o enunciado diz que o gráfico representa a onda em . Nesse instante qual é a amplitude da onda? No gráfico dado lá no enunciado vemos que em a amplitude é .
Boa, sabemos que o gráfico que representa a onda no espaço deve começar com a amplitude de , pois está é a amplitude da onda no tempo estudado.
Por isso a alternativa correta é a , pois o gráfico começa com amplitude , o que não representa a nossa onda no instante .
Resposta
Gráfico .