A figura é um gráfico-instantâneo, para , de uma onda de que se propaga para a esquerda.
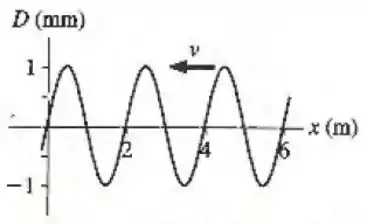
Qual é a velocidade da onda?
Qual é sua constante de fase?
Escreva a equação para os deslocamentos produzidos no meio por esta onda.
Passo 1
Bom, temos aqui um gráfico de para . Já sabemos como analisar esse gráfico.
Pelo gráfico, vemos que o comprimento de onda é .
Sendo a frequência , temos:
Passo 2
Para determinar a constante de fase, podemos analisar o gráfico. Vemos que para , temos que . Tendo em vista que é dado por:
Aqui você poderia ter usado cosseno ao invés de seno na expressão de . Se você fizesse isso, o resultado seria (testa só!)
Passo 3
Para determinar a equação da onda, vamos primeiro escrever a equação básica da onda e os valores que conhecemos:
Podemos extrair dos gráficos as seguintes informações:
A equação deve ficar assim:
Resposta