Uma onda senoidal se propaga ao longo de uma corda sob tensão. A figura 1 fornece a inclinação da corda ao longo do eixo no instante . Suponha que a equação da onda progressiva é do tipo
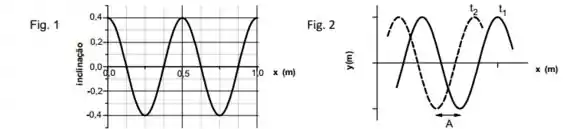
- Calcule a amplitude da onda progressiva.
- Calcule a constante de fase.
- Calcule a frequência da onda progressiva.
- Escreva a equação , com os valores pra , e , e com o sinal correto em frente a , baseando-se na análise das figuras 1 e 2.
A figura 2 mostra dois instantes diferentes de um pedaço da mesma onda progressiva da figura 1. Na figura , e
Passo 1
a)
Bom, sabemos que a função de uma onda harmônica é do tipo:
Então:
Sabemos que essa derivada tem um máximo quando:
E pelo gráfico:
Passo 2
Outra informação que podemos tirar do gráfico é acerca do comprimento de onda. Pelo gráfico, vemos que os picos se repetem a cada . Isso quer dizer que a cada a onda completa um ciclo, o que quer dizer que:
E como:
Então:
Passo 3
b)
A função da derivada nos dá:
Substituindo e :
Só que sabemos que nesse ponto temos:
Logo:
Passo 4
c)
Bom, o caminho pra se calcular a frequência passa por calcular a velocidade:
Então:
Passo 5
d)
A equação segue o padrão:
E:
Então, lembrando de todas as variáveis que calculamos:
Resposta
a)
b)
c)
d)