Uma fonte sonora emite um som que se propaga até uma ouvinte localizada a uma certa distância . Uma parede, paralela à reta ligando fonte e ouvinte, se encontra a uma certa distância de ambos (ver figura). A parede reflete o som, e a onda sonora refletida chega à ouvinte e interfere com o som que vem diretamente da fonte. A ouvinte não ouvirá som algum apenas se:
- As distâncias e forem iguais.
- A distância for um número inteiro de comprimentos de onda.
- A distância for um número ímpar de meio comprimentos de onda.
- A distância for um número inteiro de comprimentos de onda.
- A distância for um número ímpar de meio comprimentos de onda.
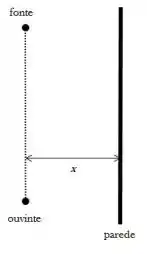
Passo 1
Cara, antes de tudo, vamos ver o que está acontecendo, beleza?
Temos uma fonte emitindo um som e uma parede do lado refletindo esse som. Temos também um ouvinte a uma distância .
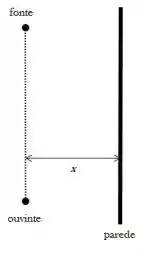
O ouvinte vai escutar dois sons: um vindo direto da fonte, e outro sendo refletido...
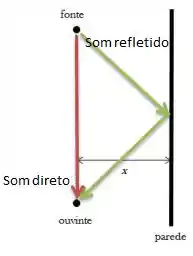
O som direto tem um caminho até a pessoa, e o som refletido tem um caminho ...
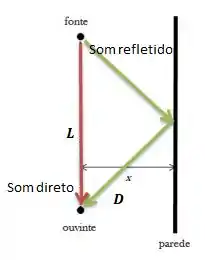
“Tá, mas por que precisamos saber sobre o caminho que o som percorre até a pessoa?”
ORA! Porque de acordo com a nossa teoria sobre interferência de ondas sonoras, duas ondas se interferem destrutivamente (de modo que o ouvinte não consegue escutar mais nada) se...
Onde é a diferença de percurso entre a onda direta e a refletida (no caso ), é o comprimento de onda da onda sonora e é um número inteiro.
Beleza! Então vamos tirar algumas conclusões sobre essa equação, pode ser?
Passo 2
Bem... Essa equação como já comentamos, nos informa quando teremos interferência destrutiva em uma onda.
Se a gente multiplicar os dois lados por ...
Ora bolas...
- é um número inteiro, ou seja... ;
- Porém, representa apenas os números ímapres, isto é
Então, outra forma de interpretar a equação do final do passo 1 é a seguinte:
Ou seja... Duas ondas se interferem destrutivamente (de modo que o ouvinte não consegue escutar mais nada) se a diferença de percurso for um múltiplo ímpar da metade do comprimento de onda.
Isso elimina aí os itens , e das possíveis respostas corretas. O que está faltando descobrir agora é justamente a diferença do percurso . Vamos nessa?
Passo 3
Já comentamos que é a diferença de percurso do som direto pelo som refletido...
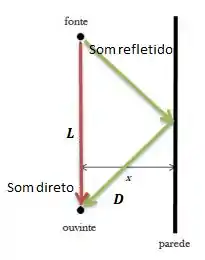
Isto é...
Só que quem é ?
Passo 4
Repare que é igual a duas vezes a hipotenusa que vou chamar de ...
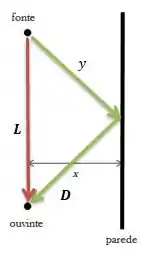
Ou seja...
Colocando essa altura ali em cima, ela dividirá a região em dois triângulos retângulos idênticos com um cateto sendo , hipotenusa e outro cateto sendo justamente a altura ...
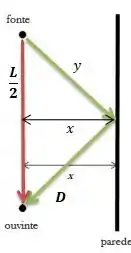
De acordo com Pitágoras então...
Ou ainda...
é então isso aí...
Como
Simplificou legal, neh?
Então, pelo passo , podemos concluir que a diferença entre o som direto e o som refletido que chega aos ouvidos do ouvinte vai ser...
E se essa diferença for um múltiplo impar da metade do comprimento de onda, então a pessoa não escutará nada da fonte.
Resposta
Letra E.