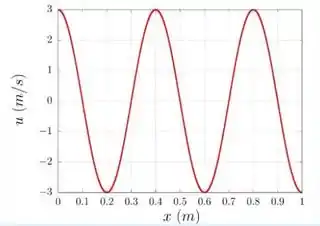
. Na figura estamos mostrando o gráfico da velocidade transversal dos pontos de uma corda na qual se propaga uma onda. O gráfico está em um estante de tempo fixo, em que é a posição do elemento da corda. Dado que a velocidade de propagação nessa corda é de , encontre a amplitude e a frequência .

. e

. e

. e

. e

. e

Vem comigo que a gente resolve essa juntos!

Para esse problema vamos lembrar de algumas expressões que envolve ondas e velocidade transversal.

Primeiro, a relação entre a velocidade de propagação da onda na corda e a frequência, dada por:

Segundo, a velocidade transversal máxima dada por:

Onde pelo gráfico temos que .

E por último a frequência angular , dada por:

Então basicamente para encontrarmos a frequência da onda e a amplitude , precisamos saber o comprimento de onda .

Para isso vamos pensar no seguinte, quando um ponto da corda tem velocidade máxima ele tem um deslocamento igual a zero e quando ele tem uma velocidade igual a zero ele tem um deslocamento máximo.

Sabendo disso e usando as informações do gráfico do enunciado podemos montar o seguinte gráfico do deslocamento de dos pontos da corda para esse instante de tempo.

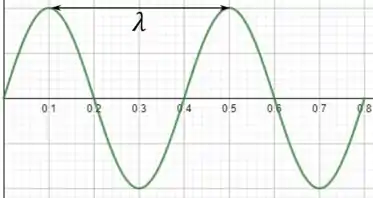
Como o comprimento de onda é a distância entre dois picos, então pelo gráfico temos que .

Agora vamos atrás do que nos interessa!