PUCRIO – Física 2 – 2020.1 – G2 – M. Escolha
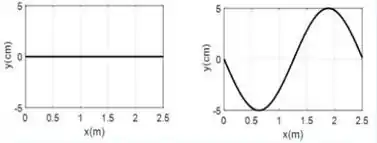
. Numa corda de comprimento , propaga-se uma onda com a seguinte função de onda:
Quais os gráficos da posição da corda nos instantes e .
.
.
.
.
.
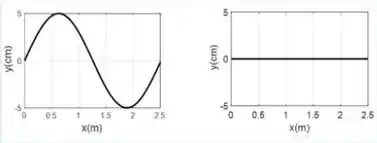
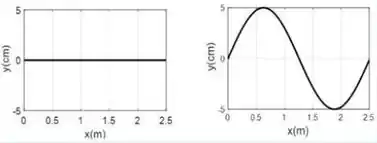
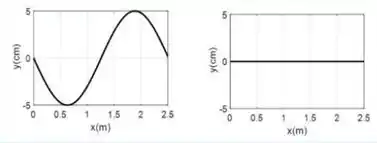
Passo 1
Vem comigo que a gente vai arrebentar com essa questão!
O enunciado nos fornece a função da onda, então temos que ver o comportamento dela para os instantes de tempo pedidos.
Mas o enunciado nos dá os intervalos de tempo em função do período , mas usando que:
E que dá função de onda temos , os instantes de tempo ficam da seguinte forma:
E para
Agora vamos avaliar a função de onda em cada um desses intervalos.
Passo 2
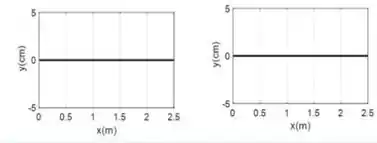
Vamos começar com , temos:
Mas como , temos que:
Logo o gráfico é uma reta constante em zero.
Passo 3
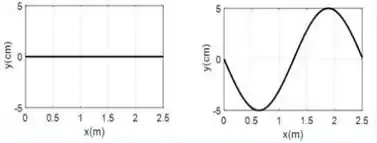
Agora vamos avaliar a função para , temos:
Mas como , temos que:
Que nos dá um gráfico da função seno só que invertido por conta do sinal.
Então temos que a alternativa que contém os gráficos corretos é a .
Resposta
.
