PUCRIO – Física 2 2020.2 – P2 – Questão 4
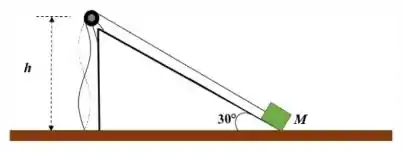
Na figura abaixo podemos verificar um plano inclinado, tanto a polia como o plano inclinado não têm atrito. A corda de comprimento total suporta um bloco de massa . Através da figura é possível notar, que o bloco de massa está na base do plano, a corda tem uma massa total , e o sistema está em equilíbrio. Considere que a massa da corda é pequena em relação à massa do bloco, note na figura, que a parte vertical da corda tem um comprimento e somente nesta região são formadas as ondas estacionárias. A aceleração da gravidade é .
- Determine a velocidade das ondas na corda.
- Determine o (comprimento de onda) da onda estacionária no segundo harmônico.
Escolha uma:
- Nenhuma das alternativas
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
A velocidade de uma corda que está submetida a uma tensão é:
E aqui temos que é a densidade linear de massa, e no nosso caso é:
Beleza até aqui?
Passo 2
Como o sistema está em equilíbrio, temos que a tensão é igual à componente horizontal do peso do bloco . Daí a tensão é:
Passo 3
Agora é só substituir na expressão da velocidade:
Passo 4
A relação entre o comprimento de onda e tamanho da corda em uma onda estacionária é:
Para o primeiro harmônico temos , para o segundo, e assim por diante. Daí temos:
E comparando com o desenho, temos que .
Analisando as alternativas, a letra certa é (f).
Espero ter ajudado!