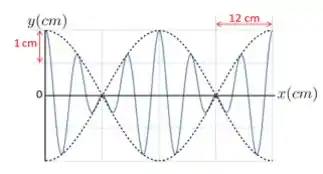
9. Duas ondas se propagam no mesmo sentido e com a mesma amplitude formando o padrão de batimento mostrado na figura abaixo. Considere , e .

Os valores de e para as duas ondas podem ser escritos como:

(a)

(b)

(c)

(d)

(e)

Olá, pessoal! Tudo bom? O enunciado nos forneeu uma figura de propagação de duas ondas e pediu para dizermos quanto vale e de cada onda.

A forma geral de duas ondas formando um padrão de batimento é:

Onde podemos observar que a função define o pacote de ondas (pontilhado) e a função define a onda propriamente dita (linha cheia). Desta forma, podemos definir como o comprimento de onda relativo à onda e como o comprimento de onda do pontilhado.

Pelo gráfico conseguimos extrair que

E

Com esses dados podemos calcular os nossos .

Bora lá!