Ao longo de uma corda de tamanho com ambas as extremidades fixas, propagam-se ondas de modo a formar uma onda resultante que obedece à expressão:
(c) No eixo fornecido a seguir, faça um esboço dessa onda no instante
d) Encontre a expressão da velocidade transversal da onda e calcule seu valor, para o instante, nos pontos , e .
Passo 1
c)
Bom, ele nos deu uma expressão e pediu o gráfico dela, quando.
Substituindo
Bom, agora é o gráfico de uma senoide. Em , teremos . O comprimento de onda dessa onda pode ser encontrado pelo argumento da função seno, já que identificando
Temos , e como , temos que
Então, a cada temos um comprimento de onda inteiro, e ele começa no .
Vamos ver se ele começa “subindo” ou “descendo”. Podemos atribuir um valor e calcular.
Para , temos:
Opa! Então, quer dizer que assim que o gráfico sai do zero, ele desce. E como temos que ter 1 comprimento de onda inteiro entre e , temos que o esboço ficará assim:
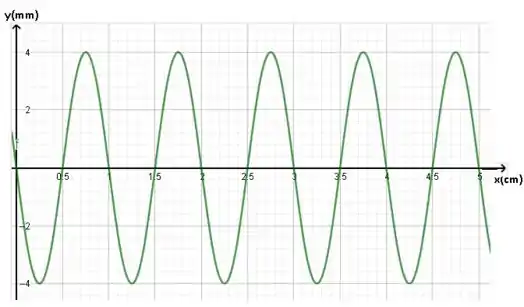
Passo 2
b)
A velocidade transversal é a derivada em relação ao tempo da equação que descreve a posição
Vou tirar as unidades pra não fiar muito poluído. Depois a gente volta e escreve tudo de novo, ok?
Eita... essa equação parece feia. Mas olha, só tem no termo com cosseno. o resto todo é constante e sai da derivada.
Pela regra da cadeia:
Em
Mas , então
Então, nesse instante, as velocidades são nulas.
Resposta
c)
d) As velocidades são nulas nesse instante.