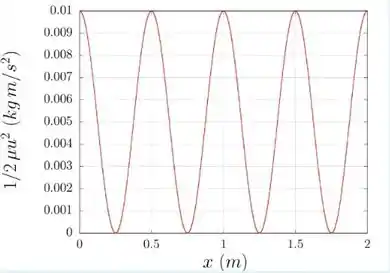
. Uma onda senoidal se propaga no sentido positivo do eixo-. Na figura estamos fornecendo a densidade de energia cinética por comprimento de uma corda no instante , onde é a posição do elemento de corda. Essa quantidade é definida como (onde o termo elevado ao quadrado, , é a velocidade transversal da onda na corda) e sua unidade é . A frequência da onda é de . Utilizando as informações do gráfico, encontre:
O comprimento de onda e o número de onda .
Se a tração for de , encontre a massa específica linear da corda.
Encontre a amplitude da onda e escreva para essa corda.
Passo 1
Vem comigo que a gente detona com essa questão!
Ela nos dá o gráfico da densidade de energia cinética em cada ponto da corda no instante . Essa densidade é dada por:
Onde é a massa específica ou densidade linear da corda e é a velocidade transversal da onda na corda, que tem a seguinte cara:
O item pede que achemos e , para isso vamos usar o gráfico ao nosso favor e encontraremos o primeira usando a equação acima e depois vamos achar , usando o fato de que:
Agora para achar a massa específica pedida em vamos usar a seguinte equação:
Onde é a velocidade da onda na corda, é a tração na corda e a massa específica que queremos encontrar. Podemos achar usando o fato de que:
Para achar a amplitude pedida em vamos usar o fato de que a velocidade máxima transversal é dada por:
E vamos usar a informação do gráfico que a densidade de energia cinética máxima é igual a e ela ocorre quando é máxima, assim:
Assim, temos:
O valor que podemos encontrar sabendo que:
Então é só calcular e achar . E depois para escrever a equação da posição é substituir o que encontramos para , que é iguala a , para e .
Vamos nessa então!
Passo 2
Começando com o item .
Olhando o gráfico vemos que em temos que a densidade de energia é zero, logo para isso acontecer temos que , assim usando a equação da velocidade temos que:
Assim, temos que:
Para que isso aconteça temos que:
Agora podemos encontrar , assim como:
Com isso temos:
Passo 3
Agora podemos começar o item .
Como falei no passo , temos a seguinte equação:
E usando que vamos isolar , temos:
Agora vamos substituir o que sabemos, temos:
E com isso temos:
Passo 4
E por último vamos para o item .
Primeiro vamos achar a amplitude, temos que:
Usando que , temos:
Agora substituindo os valores que conhecemos, temos:
Assim temos que:
Agora podemos escrever a equação da posição, ela fica da seguinte forma:
E finalizamos com sucesso esse problema!