UFMG, Sem Campus, UFMG - Problemas sobre Oscilador Harmônico, Questão 36b
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
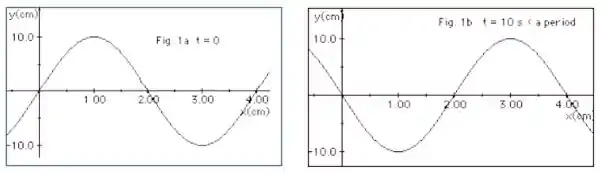
b. Nesse tempo , determine, à direita no eixo x, as duas próximas posições onde ocorrerão cristas.
Passo 1
Eaew, belezinha?
Temos que encontrar, no tempo t = 10 s, à direita no eixo x, as duas próximas posições onde ocorrerão cristas.
Então vamos lá!
Passo 2
Temos que o comprimento de onda é a medida da distância entre duas cristas, temos que , então, basta somarmos a posição da crista apresentada no gráfico para . Fazendo isso temos que as duas próximas posições que ocorrerão depois da crista na posição serão:
; .
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
; .