UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 1e
1) Determinar o domínio das funções abaixo e representá-lo no plano cartesiano.
(e)
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema, nosso objetivo é o domínio da função e fazer um esboço gráfico do seu domínio no plano cartesiano.
Parece difícil? Bora começar! 😉
Para determinar o domínio de uma função, temos que analisar a função e descobrir os possíveis valores que e são capazes de assumir para que seja definida.
Já para esboçar o gráfico do domínio, temos que verificar para quais valores de e que pertence à função ou também obter restrições do domínio e excluir essas restrições do esboço...
Sacou? Bora começar! 😁
Passo 2
A função que temos que analisar é dada por
Nesse caso temos uma fração de duas funções...
No numerador temos . Sabemos que para uma raiz existir, seu conteúdo deve ser maior ou igual a , ou seja
Já no denominador, temos . Como uma raiz não resulta em um número negativo, não é possível que o denominador de zere, logo a única restrição nesse caso é dada pela mesma ideia da restrição no numerador, ou seja
Portanto temos duas restrições para nesse caso, ele tem que ser maior que e também ser maior que .
Traduzindo isso em domínio de , temos
Bacana, não é? 😉
Passo 3
Para esboçar graficamente o domínio de , vamos olhar para as restrições e , ou seja, é definida nesses intervalos.
Na restrição , o gráfico formado é dado pelos pontos a direita da reta no plano cartesiano. Ao mesmo tempo tem que ser maior que , portanto...
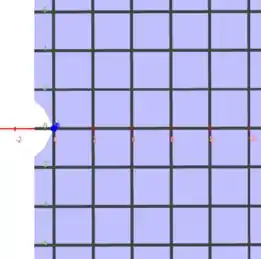
Sacou como faz? Responde Aí! 😉