UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 4a
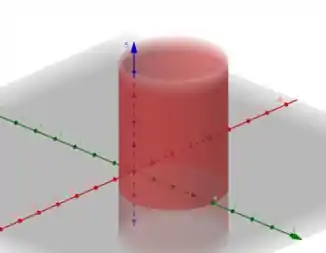
4) Faca um esboço do cilindro da equação dada:
(a) ,
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema temos apenas que esboçar o gráfico da equação no espaço.
Não parece tão difícil, não é? 😉
Nesse caso, temos que esboçar um gráfico onde uma das variáveis , ou não faz parte da equação. Com isso, o gráfico da superfície não varia nessa variável, logo podemos afirmar que o gráfico da superfície é paralelo ao eixo dessa variável.
Portanto, para esboçar o gráfico da equação, primeiro obtemos o gráfico da equação em um plano que contém as equações e depois projetar a curva formada ao longo da variável oculta.
Sacou? Bora lá! 😬
Passo 2
Nesse caso, a equação é dada por
Sabemos que essa equação é exatamente a equação da circunferência transladada no eixo
Onde é o centro da circunferência e é o raio.
Dessa forma, nossa equação resulta em uma circunferência centrada em e de raio no plano .
Projetando essa curva ao longo do eixo , vamos obter um cilindro dado por
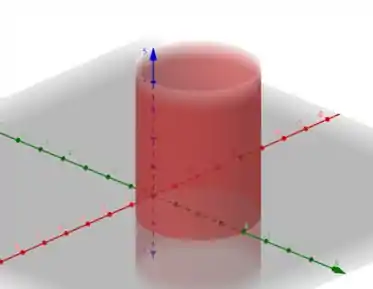
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
