UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 1h
1) Determinar o domínio das funções abaixo e representá-lo no plano cartesiano.
(h)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, nosso objetivo é o domínio da função e fazer um esboço gráfico do seu domínio no plano cartesiano.
Parece difícil? Bora começar! 😉
Para determinar o domínio de uma função, temos que analisar a função e descobrir os possíveis valores que e são capazes de assumir para que seja definida.
Já para esboçar o gráfico do domínio, temos que verificar para quais valores de e que pertence à função ou também obter restrições do domínio e excluir essas restrições do esboço...
Sacou? Bora começar! 😁
Passo 2
A função que temos que analisar é dada por
Nossa função é composta por um da função ... sabemos que só existe se , ou seja, se seu conteúdo for maior que .
Dessa forma, para ser definido, tem que ser maior que
Dessa forma, só existe se for maior que .
Traduzindo isso para o domínio de , temos
Tranquilo até aqui? 😉
Passo 3
Esboçando o domínio do domínio de graficamente, vamos olhar para a restrição
Dessa inequação, sabemos que é uma função exponencial horizontal e nossa zona de interesse é dada apenas por menor que , ou seja, graficamente o domínio de são os pontos a esquerda de
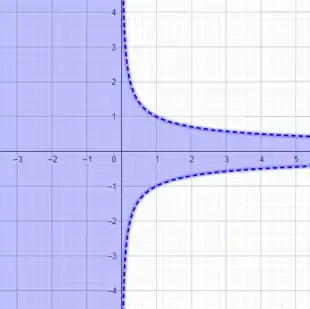
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍