UFCG, Cálculo Diferencial e Integral III, AV1, questão 1
Descreva o domínio e a imagem da função f, onde. Desenhe pelo menos três curvas de nível no domínio da função e esboce a superfície.
Passo 1
Pessoaaaaalll, oláaaa! Como estão? Precisaremos encontrar domínio, imagem, desenhar curvas de nível e esboçar a superfície dessa função. Vamos lá ver como fazer tudo, passo a passo?
Passo 2
Primeiro, vamos obter o domínio da função. Como temos uma raíz quadrada, os valores dentro dessa função devem ser maiores ou iguais a zero. Então
Resolvendo a inequação
Reescrevendo
Então o domínio será
Passo 3
Note que temos que se igualarmos a função de dentro da raíz a zero, vemos que é uma circunferência
Isso indica que seu raio é
Logo, a imagem será
Passo 4
As curvas de nível podem ser calculadas da seguinte maneira:
Elevando tudo ao quadrado
Temos então
O raio das curvas então será
Para obter as curvas, basta substituir valores para , beleza?
Abaixo temos algumas curvas possíveis:
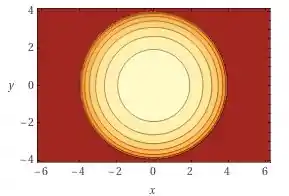
Passo 5
O esboço da superfície será:
Prontinho!
