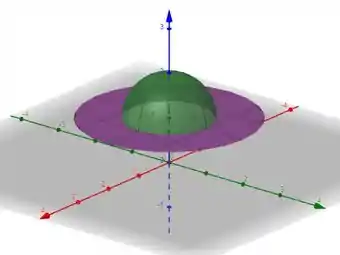
Considere a função
Definida no domínio .
Faça um esboço do gráfico de .
Passo 1
Nossa função tem duas definições, certo?
Vamos analisar uma de cada vez e depois a gente junta as coisas.
Primeiro para quando .
Identificar a superfície:
Fazer :
Essa é a equação da esfera, com centro em e raio igual a .
Passo 2
Mas como
Devemos ter . Portanto, é apenas a parte superior da esfera.
Lembrando que isso só vale para o “pedaço” do espaço que está dentro do disco .
Passo 3
Agora, quando estamos no “pedaço” do espaço em que , a nossa função assume um valor constante igual a .
Passo 4
Beleza, agora vamos juntar isso.
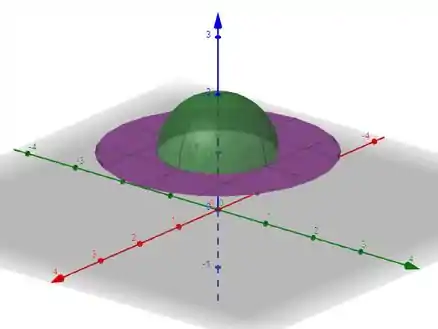
Em verde temos a parte de cima da esfera centrada em , dentro do disco e em roxo temos a nossa função com um valor constante e igual a na forma de um “CD”, ou seja, um disco com um buraco no meio, quando .
Resposta