UFAM– Cálculo 2 – P1 – Questão 1.1
Dada a função
- Determine o e
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou te ajudar aqui! Temos uma função de duas variáveis
E nesse primeiro item o problema nos pede para encontrar o domínio e a imagem dessa função.
Bom, para calcular o domínio precisamos descobrir em qual ponto essa função não está definida. E para fazer isso procuramos em duas situações
- Pontos onde há uma divisão por zero
- Pontos onde tem uma raiz de incide par de número negativo
Como não temos raiz, esse segundo ponto nós deixamos de lado!
Já a parte da divisão por zero, precisamos assegurar que o denominador não seja zero:
E isso ocorre em quase todos os pontos, menos onde . E é exatamente esse ponto que vamos tirar do domínio?
Não! Pois se trata de uma coisa do tipo
E o limite quando dessa coisa é 1! É o limite fundamental!
Sendo assim o domínio dessa função são todos os reais
Passo 2
E a imagem? Imagem é o valor que a função assume no domínio! Vamos relembrar de como é um gráfico de ?
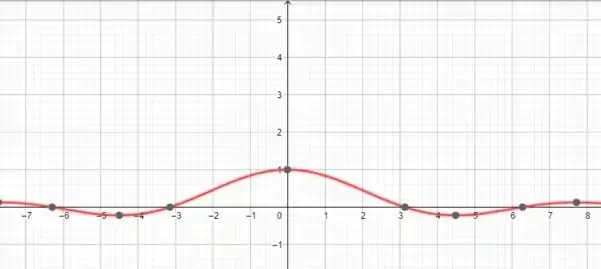
Temos que perto de a função assume seu valor máximo: 1 E depois disso ela vai gradativamente diminuindo, tendendo à zero no infinito
Será que acontece a mesma coisa com a nossa função?
Passo 3
Agora vamos dar uma olhadinha na versão 3d dessa função:
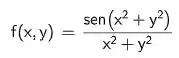
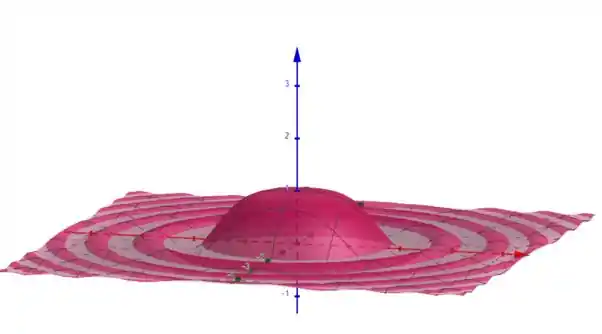
E é isso! Espero ter ajudado!
Ufa! Terminamos!
Até próxima!