Resolva o que se pede:
Determine e esboce o domínio da função
Passo 1
Opa, falou em domínio significa que temos que verificar as restrições de .
Aqui, nossa única restrição é que é temos uma função inversa da função seno.
Sabemos que o domínio da função inversa é igual a imagem da função normal.
Então, para descobrir a restrição do argumento da nossa função , que é exatamente o domínio dela, temos que pensar na restrição da imagem da função seno. Porque isso vai ser o domínio da função arco seno, sacou?
Passo 2
Vamos lá, então.
A imagem do seno a gente já tá careca de saber que varia entre e , certo?
Assim, a nossa restrição para a função inversa da função seno será que o que tá dentro do arco seno tem que estar entre e . Assim:
Daí, tiramos que
Logo, o domínio de é
Passo 3
Agora, ainda precisamos esboçar essa parada aê.
O que significa esse domínio?
Significa que
Ao mesmo tempo que
Então a gente precisa desenhar essas duas coisas e fazer a interseção entre eles. E isso será nosso domínio.
Passo 4
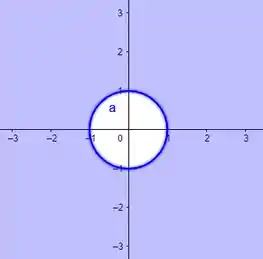
Vamos começar entendendo e esboçando:
Se fosse
Teríamos uma circunferência de raio 1, centrada na origem. Mas como temos esse sinal de “”, significa que que isso daí é como se fosse um disco, só que na real é tudo que tá pra fora dessa circunferência, inclusive sua fronteira.
Então o que essa inequação aí diz pra gente é que isso meio que é o plano todo, menos o que tá dentro da circunferência
Assim:
Passo 5
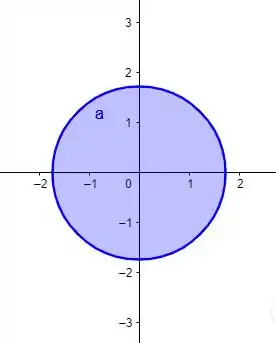
Agora vamos entender e esboçar
Se fosse
Teríamos uma circunferência de raio , centrada na origem. Mas como temos esse sinal de “”, significa que que isso daí é um disco, que compreende tudo que tá dentro da circunferência de raio , inclusive sua fronteira. Assim:
Passo 6
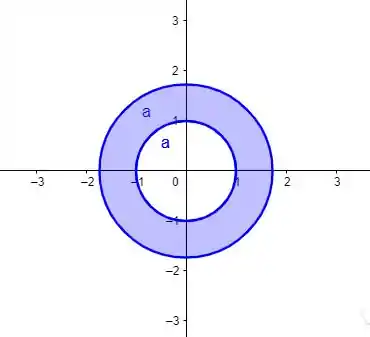
Fazendo a interseção dessas duas coisas então, temos algo do tipo
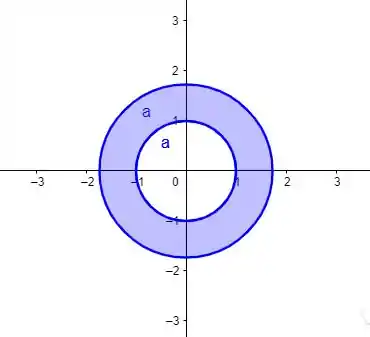
Em que o domínio seria tudo que tá dentro dessa bola rosa.
OBS: no fim das contas, como
Meio que representa o plano todo, o domínio acaba sendo só o que ta dentro do disco
(e sua fronteira inclusive).
Resposta