UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 1f
1) Determinar o domínio das funções abaixo e representá-lo no plano cartesiano.
(f)
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema, nosso objetivo é o domínio da função e fazer um esboço gráfico do seu domínio no plano cartesiano.
Parece difícil? Bora começar! 😉
Para determinar o domínio de uma função, temos que analisar a função e descobrir os possíveis valores que e são capazes de assumir para que seja definida.
Já para esboçar o gráfico do domínio, temos que verificar para quais valores de e que pertence à função ou também obter restrições do domínio e excluir essas restrições do esboço...
Sacou? Bora começar! 😁
Passo 2
A função que temos que analisar é dada por
Nesse caso temos uma raiz e sabemos que uma raiz só é definida quando seu conteúdo é maior ou igual a , ou seja
Simplificando a inequação
Dessa forma, para existir, essa inequação deve ser satisfeita. Traduzindo isso para o domínio de ...
Tranquilo até aqui? 😎
Passo 3
Agora para esboçar o domínio de graficamente, vamos olhar para a restrição .
Perceba que a inequação se parece muito com a equação de uma hipérbole horizontal
Mas como temos uma desigualdade, a região do domínio de é dada pela região em que é menor ou igual a , ou seja, a região interna da hipérbole formada por .
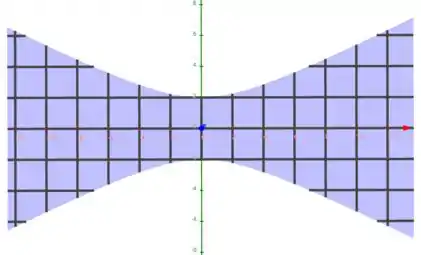
O que achou? Foi de boa? Responde aí! 😊