Considere a função
- Esboce o domínio de .
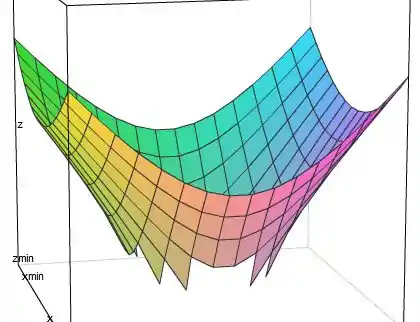
- Esboce o gráfico de determinando sua interseção com os eixos coordenados.
Passo 1
a)
Para achar o domínio temos que lembrar que o termo dentro da raiz quadrada não pode ser negativo! Com isso,
Opaa, peraí! Isso tá com cara de elipse!
De fato, temos que
é a equação de uma elipse centrada na origem e com semieixos valendo e .
Como temos uma sinal de , temos que o domínio da é tudo que está fora da elipse (ou seja, tudo que é maior ou igual a 1). Em outras palavras, será o , menos a região dentro dela.
O esboço do domínio vai ser (só vale a parte rosinha):
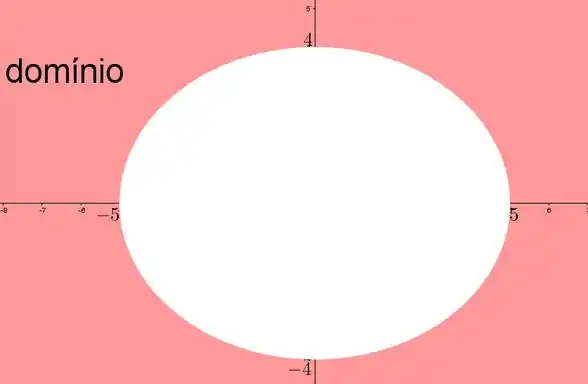
Passo 2
b)
Agora ele pediu o esboço do gráfico. Mas antes de resolver seguindo o enunciado, eu vou dar um bizu aqui!
Nosso reflexo tem que ser: chamar de ! Assim vamos ter:
Podemos elevar ao quadrado (mas tem que tomar muito cuidado com isso, vou explicar o porquê depois):
Galerinha, para quem não lembra, nós temos aqui a equação de um hiperboloide de uma folha, com eixo em . É aquele cara com forma de reator de usina nuclear:
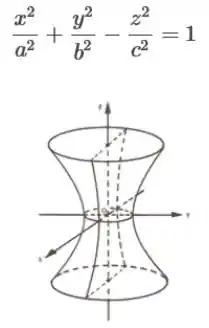
Então fica a dica, sempre bom estar com o gráfico de algumas equações na memória, pois pode ajudar muito a resolver algumas questões!
Passo 3
Mas atenção!! Até separei um passo pra isso porque é bem importante!
A nossa função de origem é
Ou seja, . Enquanto que na equação que achamos depois, do hiperboloide, admite valores negativos! Mas, repito, na nossa função não podemos ter valores negativos de .
Portanto, o nosso gráfico vai ser na verdade só metade desse hiperboloide, só a parte acima do plano !
Beleza?? Tem que ficar esperto com isso!
Passo 4
Enfim, continuando e resolvendo de acordo com o enunciado! Nós temos que seguir o procedimento padrão: analisar as interseções do gráfico com os eixos coordenados.
Vamos começar zerando a variável . Assim, podemos obter a interseção do nosso gráfico com o plano :
que é exatamente a equação da elipse que delimita o domínio da função, e que já vimos na letra a):
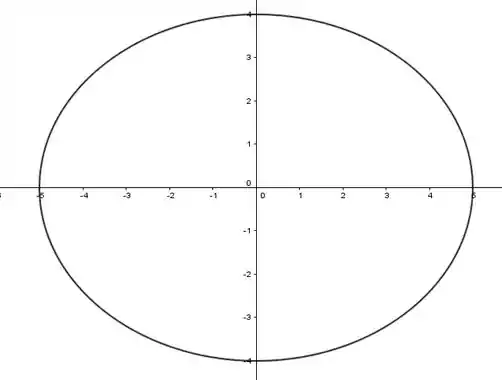
Beleza, vamos prosseguir!
Passo 5
Agora vamos zerar a variável . Vamos ter:
Opa, é agora que o nosso gráfico começa a justificar seu nome de hiperboloide! Pois isso nada mais é que a equação de uma hipérbole.
O seu esboço ficaria assim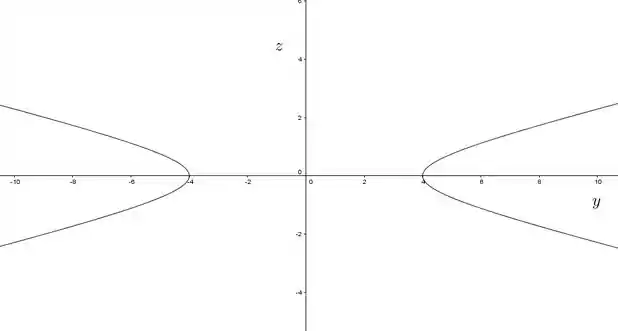
Lembrando que pro nosso gráfico só vamos considerar a parte com !!
Passo 6
Agora só falta zerar o pra ver o que tá rolando no plano :
Novamente temos uma hipérbole, que vai ser um pouco mais “pontuda” que a anterior por conta desse no lugar do :
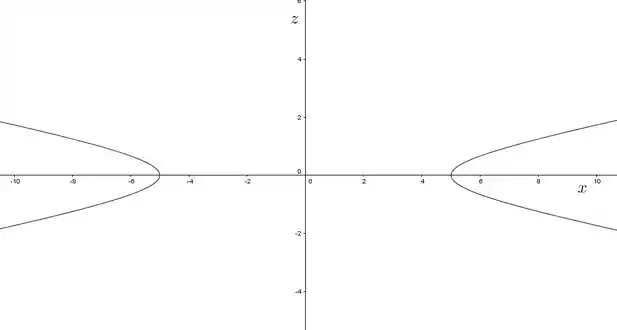
Vou repetir de novo, sou chato mesmo: pro gráfico a gente só vai usar a parte com positivo!
Passo 7
Bem agora não tem jeito, é mão na massa! A partir de isso tudo que a gente viu, com determinação deve dar pra tirar um esboço decente do gráfico! Quero ver sangue no olho, que esse gráfico é chatinho de desenhar mesmo!!
Enfim, daria alguma coisa mais ou menos assim:
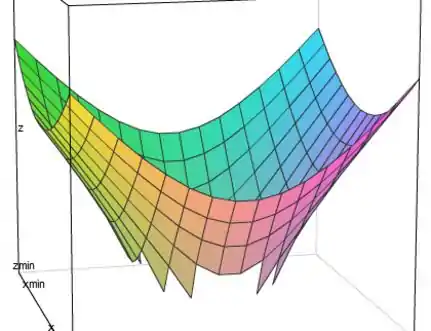
Viu, até no computador é chato de desenhar ;)
Resposta