Esboce o gráfico da função
Passo 1
Então o enunciado me deu uma função de duas variáveis , a gente pode plotar as raizes dessa equação em um terceiro eixo . Ou seja, vamos colocar nossa variável para acharmos mais facilmente o desenho dela. Chamamos então,
Agora vamos avaliar alguns planos!
Passo 2
Vale perceber que nossa função é , mas na real o não aparece nela!! Isso é um indicativo que ela tem o mesmo perfil ao longo do eixo .
Então vamos ver a curva dela no plano , anulando a variável , já que nossa função nao depende dela, lembra?
Temos uma equação de elipse que se estende por todo eixo !! Ou melhor, temos apenas a parte de cima de uma elipse, já que estamos pegando apenas e não !
Passo 3
A gente acabou de fazer o plano , mas como ficaria o plano . Para isso precisamos fazer
Olha!! Uma reta! Muito simples, na verdade... é uma reta no plano , que fica constantemente em altura ! Ele será um máximo na superfície.
Passo 4
Galera, no Passo , a gente viu que é a metade de uma elipse que se estende por todo eixo . No Passo 3, vimos que essa curva atinge um valor máximo em
Jogando isso pro gráfico, ficamos com,
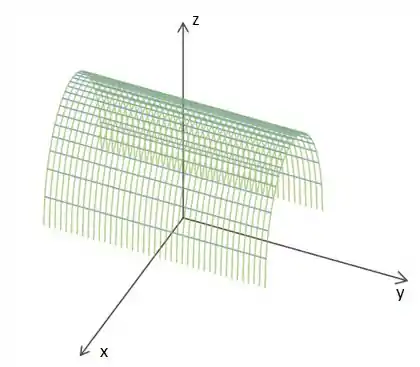
Resposta
A resposta é só repetir o gráfico acima!