UFAM – Sem campus – Cálculo II – Lista de estudos cálculo II – Lista 2 – 1i
1. Determine o domínio das funções abaixo.
i)
Passo 1
Fala aí galerinha, belezinha? Bora pra essa questão de cálculo II! Aqui a ideia pra gente achar o domínio das funções é encontrar onde ela não pode existir. A partir disso, a gente pode dizer onde ela pode existir, que é o significado de determinar o domínio da função! 😊
Mas... como a gente encontra os locais onde essa nossa função não existe?
Veja, se queremos encontrar onde ela não existe, vamos encontrar tudo que indetermina ou limita ela. Dessa forma, saberemos em quais partes do domínio dos números reais ela não pertence. Se liga no próximo passo que eu te mostro!
Passo 2
Bem, temos uma divisão dentro da função, então vamos dividir em duas partes pra entendermos essa restrição.
Bem, para o numerador não existe nada que restringe essa função. Qualquer valor de ou pode entrar no numerador que tá tranquilo. O problema (ou a solução) tá no denominador.
Passo 3
O denominador da nossa função se trata de:
Pra essa função existir, o único jeito é se o denominador for diferente de 0. Escrevendo isso matematicamente, temos que:
Ou seja,
Somente nesses casos que a nossa função não vai existir.
Passo 4
Belezinha, agora pra gente fechar com chave de ouro, precisamos escrever isso matematicamente. Expressaremos no seguinte formato: a função existe em todo conjunto dos reais (em duas dimensões), contanto que seja diferente de ;
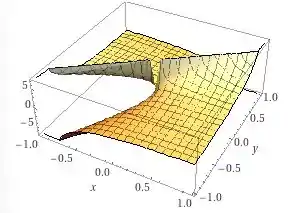
Dando uma olhadinha no Wolfram pra gente visualizar o domínio graficamente:
Curtiu a questão? Ainda restou alguma dúvida? Dá um feedback pra gente