UFF, Sem Campus, Cálculo IIB, P1 - Profº Leonardo - 2018.2, Questão 1a
(1) Seja .
a) Descreva e esboce o domínio .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos que obter o domínio da função .
Parece simples, não é? 😊
O domínio de uma função nada mais é do que os possíveis valores que ela pode admitir.
Ou seja, o domínio de é o conjunto numérico que e podem admitir para que seja definida.
Sacou? Bora começar! 😉
Passo 2
Analisando a função , vemos que se trata de uma fração onde no numerador temos a constante e no denominador temos uma raiz .
Para uma raiz ser definida, sabemos que seu conteúdo deve ser maior ou igual a , porém, por estar no denominador de uma fração, se a raiz resultar em , a função não será definida.
Portanto, para ser definida, o conteúdo dentro da raiz tem que ser maior que , ou seja
Ou seja, encontramos um círculo de raio .
Escrevendo o domínio de ...
Por último, esboçando o domínio de através da restriç��o
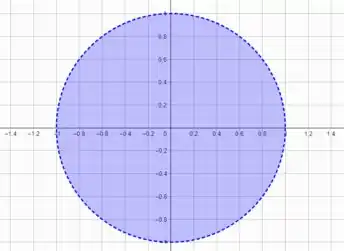
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍