UFSC, Joinville, Cálculo II, P2 - 2022.2, Questão 2a
2. Considere a função .
a) Determine e esboce o domínio de .
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema foi dada uma função onde
A partir dessa função queremos descobrir e esboçar seu domínio.
Lembra como fazemos isso? 🤔
Para obter o domínio de uma função temos que analisar a função em si e ver quais são as restrições que tem nela.
Eu seja, temos que analisar quais os possíveis valores que e não podem assumir para que seja definida.
Sacou? Bora começar! 😉
Passo 2
A função é dada por
Nesse caso sabemos que a função só é definida quando seu valor interno é maior que .
Dessa forma o conteúdo dentro do tem que ser maior que para que seja definida, ou seja
Portanto o domínio de é obtido como
Sabemos que é uma circunferência centrada na origem e com raio , mas nossa região de domínio é a região onde é maior que , ou seja, a região externa à circunferência.
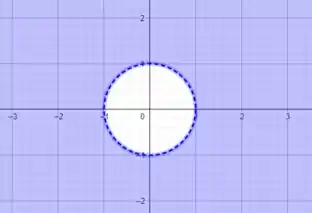
Sacou como faz? Responde Aí! 😉