UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 1j
1) Determinar o domínio das funções abaixo e representá-lo no plano cartesiano.
(j)
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema, nosso objetivo é o domínio da função e fazer um esboço gráfico do seu domínio no plano cartesiano.
Parece difícil? Bora começar! 😉
Para determinar o domínio de uma função, temos que analisar a função e descobrir os possíveis valores que e são capazes de assumir para que seja definida.
Já para esboçar o gráfico do domínio, temos que verificar para quais valores de e que pertence à função ou também obter restrições do domínio e excluir essas restrições do esboço...
Sacou? Bora começar! 😁
Passo 2
A função que temos que analisar é dada por
Podemos perceber que nossa função é composta por uma fração de duas funções.
No numerador temos ... nesse caso não há restrições para e , então essas variáveis podem assumir qualquer valor até agora.
No denominador temos , então como temos uma raiz, o conteúdo dentro da raiz deve ser maior ou igual a , mas por estar no denominador, não podemos ter , então o que temos é
Traduzindo essas informações para o domínio de , temos
Tranquilo até aqui? 😎
Passo 3
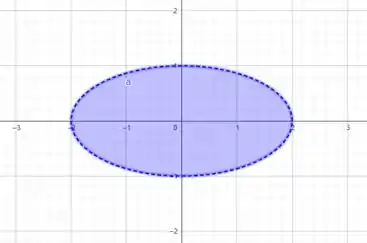
Agora vamos esboçar a região do domínio de e para isso vamos ver a restrição
Essa inequação parece muito com a equação da elipse
Adaptando nossa inequação, temos
Como temos um sinal de , nossa região compreende a parte interna da elipse, ou seja
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí